河原林巨大グラフプロジェクト

研究総括　河原林　健一

研究総括　河原林健一
（国立情報学研究所情報学プリンシプル研究系　教授）
研究期間：2012年10月～2018年3月
特別重点期間：2018年4月～2019年3月
グラント番号：JPMJER1201

インターネットのWeb構造や、Facebook、Twitterなどのソーシャルネットワークに代表される巨大なネットワークは、各々10⁹（10億人）に近いユーザーが利用し、現代社会に欠かせない存在となっています。これらのネットワークは年々急速に膨張し、近い将来には10¹⁰を超えるサイズになると予想されています。

ネットワークの膨張に伴う情報量の増大はハードウェアの進歩を上回る速さで進んでおり、いわゆる「ビッグデータ」の中でも特に巨大な、10¹⁰以上のサイズのネットワークに対しては、現行のアルゴリズムでは実用的な速度で情報を解析することが不可能であり、高速アルゴリズムの開発が急務となっています。

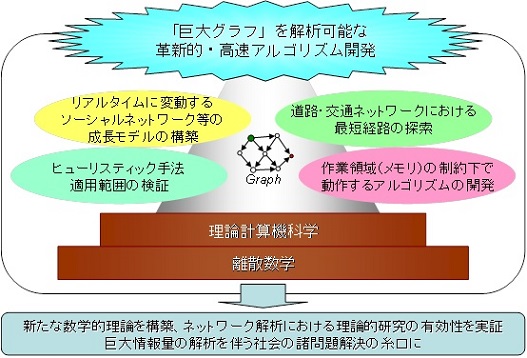
このような背景のもと、本研究領域では、巨大なネットワークを膨大な点と辺の接続構造、すなわち10¹⁰以上の頂点を持つ「巨大グラフ」として表現し、理論計算機科学や離散数学などにおける最先端の数学的理論を駆使してそれを解析する、高速アルゴリズムの開発を目指します。

具体的には、次の4つのテーマに取り組みます。①巨大な道路・交通ネットワークにおける2点間の最短経路の探索に関して、最新の理論的研究に基づいた前処理アルゴリズムを開発し、実用的なサイズのデータ構造を予め作成することで短時間に探索結果を得ることを目指します。②リアルタイムで変化・膨張を続けることから、モデル化や解析が非常に困難なWeb構造やソーシャルネットワークについて、その近未来を予測する成長モデルの構築を図ります。③携帯電話や個人利用のPCなど、解析に高性能コンピュータ（HPC）を利用できない環境を考慮して、作業メモリに制限のある状況下でも高速計算の可能なアルゴリズムを作成します。④アルゴリズムの高速化に寄与するとされる、ヒューリスティック手法（正解である保証はないが、経験則などを用いて、ある程度のレベルで正解に近い解が得られる方法）の巨大ネットワーク解析における適用範囲について、理論的な検証を行います。これらの研究を通じて、新たな数学的理論を構築するだけでなく、ネットワーク解析における理論的研究の有効性を実証し、交通網やWebの解析に加えて、バイオインフォマティクスや、災害時における有効な情報伝達方法の解析手段となるなど、巨大な情報量のために従来の手法では対処できなかった諸問題解決の糸口を得ることを目標とします。

本研究領域は、センシングデータなど、大量の情報を解析して個人に必要かつ最適な作用・効果を提供する環境の実現にも寄与するものであり、戦略目標「人間と調和する情報環境を実現する基盤技術の創出」に資するものと期待されます。

fig1

研究成果の概要

本プロジェクトは、コンピュータサイエンス分野での研究経験がない若手の研究者集団が、数学的理論研究を追及することによって理論計算機科学、離散数学、最適化、アルゴリズム分野のみならず、コンピュータサイエンスの様々な分野（機械学習、人工知能、データベース、データマイ二ング、自然言語等）のトップ国際会議に論文発表が可能になることを国内外に示し、以下の著しい成果を挙げた。

コンピューターサイエンス分野のトップ国際会議に120本を越える論文が採択された。コンピュータサイエンス分野のトップ国際会議において本プロジェクトから採用された論文数は、各々のトップ国際会議の日本全体から採用された論文数の２分の1から５分の１を占めている。また理論計算機科学、離散数学、アルゴリズム分野のトップ国際会議では、本プロジェクトから採用された論文が、日本全体から採用された論文の大半を占めている状況である。
SODA 2013、SODA 2015、FOCS 2015、STOC 2017の理論計算機科学のトップ国際会議4つで最優秀論文賞（Best Paper Award）を受賞した。また、出身者がFOCS 2018の最優秀賞学生論文賞（Best Student Paper Award）を受賞した。STOC, FOCS, SODAは理論計算機科学、アルゴリズム分野の最高峰の国際会議であり、これらの会議での最優秀論文賞（Best Paper Award）は、当該年度の最優秀論文と認定されたことを意味する。
理論計算機科学分野のトップ国際学術雑誌 SIAM Journal on Computing、ACM Transaction on Algorithmsにあわせて7本以上の論文が採択された。また組合せ論分野のトップ国際学術雑誌 Journal of Combinatorial Theory Series B, Combinatorica, SIAM Journal on Discrete Mathematics, Random Structures and Algorithmsに合計50本以上の論文が採択された。理論計算機科学、離散数学、アルゴリズム分野でのトップ国際学術雑誌に毎年10本近くの論文が採用されており、本プロジェクトは当該分野で世界でも有数の研究組織として認知された。
Journal of the ACM（JACM:コンピュータサイエンス分野の世界最高水準の国際学術雑誌）などの分野トップ国際学術雑誌に３本の論文が受理された。

なお、本プロジェクトはグラフマイニング&Web&AI（以下マイニンググループ）、複雑ネットワーク・地図グラフ（以下複雑グループ）、グラフ・ネットワークにおける理論と最適化（以下理論グループ）、ネットワーク・アルゴリズム（以下ネットワークグループ）の4グループの体制で研究を推進した。

研究成果

A. グラフの連結度に関する研究成果

Ken-ichi Kawarabayashi and Mikkel Thorup, Deterministic Edge-connectivity of a Simple Graph in Near-Linear Time, Journal of the ACM，Volume 66, Issue 1, (2019), Article No. 4，2019年1月

この論文は国際会議 STOC 2015に採択された。この論文の国際学術雑誌版は、2015年9月にコンピュータサイエンス分野の最高峰の国際学術雑誌 Journal of the ACM（J. ACM）に投稿され、最近受理された。論文の内容はグラフ（ネットワーク）の連結度に関する結果である。グラフの連結度を求める問題は、東西冷戦時代（つまり1950年代）より組合せ最適化における中心的課題の一つである。本論文では辺連結度に関して、初の「決定的」線形アルゴリズムを与えた。辺連結度に関する「非決定的」線形アルゴリズムは、Kargerにより2000年に開発されていたが、「決定的」アルゴリズムは長年未解決であった。本論文はその最終的な解決を与えている。

B. グラフ彩色に関する研究成果

Ken-ichi Kawarabayashi and Mikkel Thorp, Coloring 3-colorable graphs with o(n^{1/5}) colors, Journal of the ACM，Volume 64 Issue 1, （2017), Article No. 4，2017年3月

この論文は国際会議 Annual Symposium on Foundations of Computer Science（FOCS 2012）に採用された。この論文の国際学術雑誌版は、2012年9月にJ. ACMに投稿され、受理された。論文の内容は、グラフ彩色問題における「3色問題」に関する結果である。与えられたグラフの3彩色性の判定は、有名なNP困難問題の一つとして知られている。このような状況のもと、与えられたグラフは１）3彩色可能でないか、２）ｋ色で彩色可能であるかを多項式時間で判定する問題は、過去30年にわたり、グラフ彩色問題の中での中心的課題であった。実際Wigderson, Sudanなどのネバンリンナ賞受賞者や、Blum, Arora, Kargerなどの世界的研究者が長年取り組んだ問題である。本論文では、10年ぶりの本質的改良を与えた。過去20年間にわたってこの問題の研究手法であったSemi-Definite Programingに基づく改良ではなく、本論文はグラフ理論的なアイデアに基づく改良であり、その点も世界的に評価されている。

C. 2部クリークの固定パラメータ困難性に関する研究成果（固定パラメータ計算理論の重要な未解決問題の解決）

Bingkai Lin, The Parameterized Complexity of k-Biclique, Journal of the ACM Volume 65 Issue 5, (2018), Article No. 34 ，2018年9月（理論グループの研究成果）

k-2部クリーク問題とは、グラフがサイズk×kの完全二部グラフを部分グラフとして持つかを判定する問題である。この問題の計算複雑度がW[1]困難かどうかは、固定パラメータ計算量理論において長年未解決であり、DowneyとFellowsによる当該分野の著名な教科書にも重要な未解決問題のひとつとしてあげられている。本研究では、サイズkのクリークを見つける問題を、2部クリークでサイズがkのみに依存するものを見つける問題に帰着することで、この予想を肯定的に解決した。帰着先のパラメータのサイズは、決定的な手法ではk!、乱択手法ではより小さなk^2となる。これにより、乱択ETHなどの妥当な仮定のもとでは、k-2部クリーク問題はf(k)^o(√k)時間で計算不能であることが言える。この結果は、その重要性からSODA　2015の最優秀論文賞（Best Paper Award）を受賞している。

D. 向きつけグラフに関する研究成果（グラフ理論における20年来の未解決問題の完全解決）

Ken-ichi Kawarabayashi and Stephan Kreutzer, The Directed Grid Theorem. Proceedings of the Forty-Seventh Annual ACM on Symposium on Theory of Computing, STOC 2015, Portland, OR, USA, June 14-17, 2015, 655-664.

（向きがない）グラフ上で定義された「木幅」に関する研究は、80年代の離散数学で最も深淵とされている「グラフマイナー理論」の発展とともに、近年のアルゴリズム分野・離散数学分野での中心的課題となってきた。本研究は、1990年代中盤にReed, Robertson, Seymour, Thomasなどの著名な数学者によって予想された「向き付きグラフの木幅とグリッドマイナーのMin-Max予想」の完全解決である。この結果により「グラフマイナー理論」の向き付きグラフへの拡張が可能になると考えられている。本研究成果は、国際会議STOCに2015年に会議版として採用された。そしてこの論文の学術雑誌版は、2015年9月に数学分野の最高峰の学術雑誌のひとつである「J. AMS (American Mathematics Society)」に投稿され、編集者から条件付き受理と修正版の要請があり、今後修正版が同誌に発表される予定である。

E．グラフ分解に関する研究成果（アルゴリズムグラフ理論の指導原理に対する本質的貢献）

Martin Grohe, Ken-ichi Kawarabayashi, and Bruce Reed, A Simple Algorithm for the Graph Minor Decomposition - Logic meets Structural Graph Theory, ACM-SIAM Symposium on Discrete Algorithms, (SODA 2013), 414—431.

1980年代より、RobertsonとSeymour離散数学におけるもっとも深淵であり、インパクトのある「グラフマイナー理論」における一番の研究成果は「グラフマイナー分解定理」であると言われている。実際この分解定理が、アルゴリズム分野、理論計算機分野、離散数学分野などの様々分野で応用されてきた。しかしながら、この分解を効率的にどのようにあたえるか？という問題は未解決であった。本研究ではこの未解決問題に対して完全解決を与えている。研究手法は、数理論理分野の手法と離散数学の手法をうまく組み合わせている。研究成果のインパクトのみならず、研究手法も評価され、本論文は、SODA 2013にて最優秀論文賞（Best Paper Award）を受賞した。

F．計算理論に関する研究成果（計算理論における20年以上の未解決問題に対する本質的貢献）

Benjamin Rossman, Rocco A. Servedio, Li-Yang Tan. An Average-Case Depth Hierarchy Theorem for Boolean Circuits, Proceedings of the 56th Annual IEEE Symposium on Foundations of Computer Science (FOCS 2015), 1030-1048, （理論グループの成果）

深さが定数である回路の計算量は古くから盛んに研究されており、ある関数に対する回路計算量の指数下界が示されているだけではなく、その証明手法は疑似乱数、計算学習理論、証明の複雑さの理論などさまざまな理論で利用されている。本研究では、深さdの回路と深さd-1以下の回路の計算能力の違いを、「平均時深さ階層定理」を示すことで明らかにした。この定理は、平均時解析においても、深さdの回路と深さd-1以下の回路のあいだに指数的な計算量の差があることを示しており、1980年代に示された深さ階層定理の平均時への拡張である。この結果によって1986年にHåstadによって挙げられた未解決問題が解決された。さらに、この定理は多項式階層とも関連が深い。構造的計算量理論において「多項式階層が全て異なる」という予想が、P≠NPよりも強い予想として広く信じられている。本研究では「平均時深さ階層定理」の応用として、ほとんど全ての神託Aに対して、Aによって相対化された世界では、多項式階層が全て異なることを示した。この結果は1980年代から知られているHåstad, Cai, Babaiの予想を肯定的に解決したものであり、神託がない場合にも予想が成り立つことを示唆する重要な結果である。その研究の価値が評価され、本論文はFOCS 2015の最優秀論文賞（Best Paper Award）に選ばれている。

G．Twitterの情報のアップデータに関する研究成果（ソーシャルネットーワークにおいて社会的にインパクトのある研究成果）

Kohei Hayashi, Takanori Maehara, Masashi Toyoda, & Ken-ichi Kawarabayashi, Real-Time Top-R Topic Detection on Twitter with Topic Hijack Filtering. Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD 2015), 417―426（マイニンググループと理論グループの共同研究による研究成果）

ソーシャルネットワークサービスの一種であるTwitterのユーザ数は世界中で3億人を超えており、共有される情報量は極めて大きいが、データの巨大性からどのような情報が今話題になっているかを知ることは難しい問題となっている。また有意義な情報に混じり、広告やいわゆるスパムも一定の割合で含まれているため、これらを除去できる方法が望まれる。本研究では、Twitterデータから、現在話題となっているトピックを抽出するモデルおよびアルゴリズムを開発した。この研究ではTwitterに流れる情報を非負行列分解（NMF）により単語とユーザのクラスタリングを逐次行うことで動的にトピックを抽出する。また抽出したトピックは単語の頻度分布としても解釈可能であり、この性質を使って、得られたトピックが人工的に作られたものかどうかを統計的検定により識別し、自動的に取り除くことができる。計算機実験にて実ツイートデータを用い、既存手法より数百倍高速にかつ精度よくトピックが抽出できることを確認した。

H．最短路クエリに対する研究成果（最短クエリに関して、現在世界最速のアルゴリズムの開発）

Takuya Akiba, Yoichi Iwata, and Yuichi Yoshida. Fast exact shortest-path distance queries on large networks by pruned land mark. Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data (SIGMOD 2013), 349-360.

Takuya Akiba, Yoichi Iwata, and Yuichi Yoshida. Dynamic and Historical Shortest-Path Distance Queries on Large Evolving Networks by Pruned Landmark Labeling, Proceedings of the 23rd International Conference on World Wide Web (WWW 2014), 237-248. （複雑グループの研究成果）

最短距離クエリとは、グラフの二点を指定し、その間のグラフ上の距離を問うクエリのことである。本研究の手法では数億辺程度の複雑ネットワークから数時間で索引を作成することができる。これにより既存の索引手法に比べて数十倍の規模のネットワークを扱うことが可能となった。また索引によりクエリに数マイクロ秒で答えることが可能である。本研究の手法は非常に単純な枝刈り探索に基づいているが、複雑ネットワークの構造を極めて上手く利用している。複雑ネットワークにはハブと呼ばれる多くの最短路が通る頂点が存在することが知られているが、その様な頂点が存在すれば索引の大きさが抑えられることが説明できる。また、複雑ネットワークの周辺部は木に近い構造をしていることが知られているが、その様な場合にも索引の大きさが小さくなることを理論的に証明できる。

I. 類似度検索（SIMRANK）に関する研究成果（類似検索において、現在世界最速アルゴリズムの開発）

Mitsuru Kusumoto, Takanori Maehara and Ken-ichi Kawarabayashi, Scalable similarity search for SimRank, Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data (SIGMOD 2014), (2014), 325-336.

Takanori Maehara, Mitsuru Kusumoto, and Ken-ichi Kawarabayashi. Scalable SimRank join algorithm, Proceedings of the 31st IEEE International Conference on Data Engineering (ICDE 2015), 603―614. （複雑グループと理論グループの共同研究による研究成果）

頂点の類似度検索に用いられるSimRankは、二点間の類似度を測る指標である。SimRankは類似ページ検索以外にも、類似遺伝子検索、類似単語検索など様々な他分野に応用されてきた。しかしながらSimRankを計算するためには、計算量O(nm)必要（nは与えられたグラフの頂点数、mは与えられてグラフの辺数）になる、という問題があった。本研究では、計算時間O(m)のアルゴリズムを開発することに成功した。SimRankの定義は行列の形で書くことが出来るが、線形演算ではない演算が存在するため、計算が困難であった。そこで本研究ではSimRankというnに関して2乗個の変数以外に線形個の「ダミー変数」を導入することにより、演算をすべて線形にする定式化を提案した。この定式化により、Gauss-Seidel法と呼ばれる数値計算的に線形連立方程式を反復法で解く手法を応用することが可能になり、SimRankも計算することが可能になった。この手法により、これまで数十万辺のグラフに対して、数時間必要であったSimRank計算が、数秒で計算可能になった。また数時間の計算により、１億辺以上の大規模グラフに対応することが可能となった。

J. PageRank計算の高速化（Google最大の発明であるPageRankに対して、現在世界最速アルゴリズムの開発）

Takanori Maehara, Takuya Akiba, Yoichi Iwata and Ken-ichi Kawarabayashi, Computing personalized PageRank quickly by exploiting graph structures, Proceedings of the 40th International Conference on Very Large Data Bases, (2014), 1023-1034.

Naoto Ohsaka, Takanori Maehara, and Ken-ichi Kawarabayashi, Efficient PageRank Tracking in Evolving Networks, 21st ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD 2015)（複雑グループと理論グループの共同研究による研究成果）

PageRankを実世界のネットワークの構造を利用して計算するアルゴリズムを提案した研究成果である。この研究では、最初にソーシャルネットワークやウェブグラフなどの複雑ネットワークが、ランダムグラフの様な「コア」部分と、木の様な形をした部分に分けられることをまず確認し、前者にはKrylov Subspace Methodと呼ばれる現代的に連立方程式を解く手法を適用し、後者にはガウスの消去法と呼ばれる古典的な連立方程式を解く手法を適用することで、全体として高速なアルゴリズムを得ることに成功している。

K．機械学習と性質検査（機械学習分野に、「性質検査」という概念を初めて導入）

Kohei Hayashi and Yuichi Yoshida, Minimizing Quadratic Functions in Constant Time, Neural Information Processing Systems (NIPS 2016).（マイニンググループと複雑グループの共同研究による研究成果）

機械学習の様々な問題は、一般に連続な変数を引数とする目的関数の最小化として定式化される。なかでも目的関数が二次形式で記述されるケースは非常に多く、例えば線形回帰の問題がこれに含まれる。一般に二次形式の厳密な最小化には、変数の数をnとすると、nの多項式時間かかることが知られている。nは問題によっては非常に大きくなるため、この計算量の削減は応用上大きな意義がある。本研究では、サンプリング法を用いて二次形式の最小化をnに依存しない定数時間で近似的に解くアルゴリズムを提案した。また得られる近似最小値の誤差について理論的に上限を評価し、これが数値実験結果と整合することを確かめた。なお、本研究は計算機科学の分野で知られている性質検査のアイデアを機械学習に結びつけた世界でも珍しい研究であり、同じ方向性の研究が今後盛り上がることが期待される。

L．ネットワークルーティングに関する研究成果（計算幾何ベースによるオンラインルーティングの高速化）

N. Bonichon, P. Bose, J.-L. De Carufel, L. Perković, and André van Renssen. Upper and Lower Bounds for Online Routing on Delaunay Triangulations. Discrete & Computational Geometry, 2016.

Prosenjit Bose, Rolf Fagerberg, André van Renssen, Sander Verdonschot. Optimal Local Routing on Delaunay Triangulations Defined by Empty Equilateral Triangles. SIAM J. Comput. 44(6): 1626-1649(2015)（ネットワークグループの研究成果）

ルーティングは巨大なネットワークにおける基本的な問題である。ネットワークの各ノードは全体の情報を持っていないため、遠く離れたノードにメッセージを送ろうとするとき、まずは近いノードへメッセージを送ると同時に、そのノードにメッセージの送信を依頼を繰り返し、指定のノードまでメッセージを送る。しかし、どんなネットワークにおいても確実にメッセージ送信をすることができる既存のルーティング・アルゴリズムはごくわずかである。本研究では、幾つかの基本的なネットワーク群に対する斬新なルーティング戦略を提案した。この戦略を用いることにより、確実に目的地までメッセージを運ぶだけでなく、メッセージ送信の際に遠回りすることを回避することが可能となった。

M．通信ネットワーク設計に関する研究成果（通信コストと通信容易性に特化したネットワークの提案）

P. Bose, J.-L. De Carufel, P. Morin, André van Renssen, and S. Verdonschot. Towards Tight Bounds on Theta-Graphs: More is not Always Better. Theoretical Computer Science (TCS 2016), 616:70-93.（ネットワークグループの研究成果）

巨大な通信ネットワークを設計することは容易な仕事ではない。本研究では、通信の容易性とコストの間のバランスを取るようなネットワークであるシータグラフを提案した。これらのグラフは疎であり、直接に接続されるノード対の数は多くなく、建設及び維持に必要なコストを低く抑えられる。さらに、通信が容易にできることを証明した。とくに、任意の2つのノードをつなぐパスの長さに対する理論的な解析を行った。

N. グラフ極限理論の応用

Masaaki Imaizumi, Takanori Maehara and Yuichi Yoshida [21st International Conference on Artificial Intelligence and Statistics (AISTATS 2018)]　（複雑グループとグ理論グループの共同研究による研究成果）

統計学の基本的な問題である確率密度推定に対しグラフ極限理論を適用した。確率密度推定には多数の既存手法があるが、そのすべてにおいて確率密度関数が連続かつ微分可能であることを仮定している。それに対して提案手法では確率密度関数が微分不能であっても正しく動作することを示し、またそれにより得られる収束レート（確立分布からのサンプル数と確率密度推定の際の誤差の関係）がそれ以上改善できない、即ちどのようなアルゴリズムを持ってきてもより良い収束レートは達成できないことを示した。本結果はAISTATS 2018においてBest Paper Awardに選ばれている。

O. 重み付き線形マトロイドパリティ問題に対する多項式時間アルゴリズム（アルゴリズム分野における30年以上の未解決問題の解決）

Satoru Iwata and Yusuke Kobayashi: A weighted linear matroid parity algorithm, Proceedings of the 49th ACM Symposium on Theory of Computing (STOC 2017), 2017（理論グループの成果）

重み付き線形マトロイドパリティ問題と呼ばれる最適化問題に対して、初の多項式時間アルゴリズムを与えた。線形マトロイドパリティ問題は、組合せ最適化における代表的な問題であるマッチング問題と線形マトロイド交差問題の共通の一般化として提案された問題であり、1970年代に多項式時間アルゴリズムが与えられている。マッチングやマトロイド交差については、各要素に「重み」の付いた問題に対しても多項式時間アルゴリズムが知られていることから、重み付きの線形マトロイドパリティ問題に対しても同様に多項式時間アルゴリズムが存在するのではないかと長い間予想されてきた。本研究は30年以上未解決だったこの問題を肯定的に解決するものであり、多項式時間で解ける組合せ最適化問題の限界を推し進める成果であると言える。30年以上の未解決問題を解決した点が高く評価され、STOC 2017の最優秀論文賞（Best Paper Award）を受賞した。

P. 因果バンディット問題に対する効率的アルゴリズム

Akihiro Yabe, Daisuke Hatano, Hanna Sumita, Shinji Ito, Naonori Kakimura, Takuro Fukunaga, Ken-ichi Kawarabayashi, Causal Bandits with Propagating Inference, Proceedings of the 35th International Conference on Machine Learning (ICML 2018)　（マイニンググループと理論グループの共同研究による研究成果）

バンディットとは、web広告の候補などの戦略集合が与えられたときに、新規戦略の探索と、暫定的な有力戦略の施行による利得の獲得のトレードオフをとるアルゴリズムの枠組みである。因果バンディット問題においては、戦略と利得の関連性を表す因果グラフが追加知識として与えられた場合に、一般のバンディットに比べて効率的な探索を行うことを目指す。既存研究[Lattimore らNIPS 2016]においては、深さ１の因果グラフの構造に対してのみ、有効なアルゴリズムが提案されていた。本論文では、いかなる深さの因果グラフにも適用できる因果バンディットアルゴリズムを提案し、指数的に大きな戦略集合に対しても効率的に探索を行うことができることを示した。なお、この研究はNECとの共同研究である。

Q. サイズ制約つきオンラインポートフォリオ選択アルゴリズムと最悪ケース解析

Shinji Ito, Daisuke Hatano, Hanna Sumita, Akihiro Yabe, Takuro Fukunaga, Naonori Kakimura, Ken-ichi Kawarabayashi, Regret Bounds for Online Portfolio Selection with a Cardinality Constraint, Proceedings of the 32nd Annual Conference on Neural Information Processing Systems (NIPS 2018)（マイニンググループと理論グループの共同研究による研究成果）

オンラインポートフォリオ選択は、逐次的な意思決定問題の一種であり、価値が変化する資産の配分・投資比率を繰り返し調整して長期的な利益の最大化を目指す問題である。この問題に対しては、ある意味で最適な意思決定を実現する多項式時間アルゴリズムが知られている。一方で、現実の応用例においては投資可能な資産の組合せに制約がある状況が考えられるが、そのような制約付きの問題に直接適用できる方法は知られていなかった。本研究では、投資可能な資産の組合せが制限されたオンラインポートフォリオ問題を扱い、劣線形リグレットを達成する、つまり最善の固定戦略と同等の効果に漸近することが保証されたアルゴリズムを提案した。加えて、最悪ケースにおける損失の下界を評価することで、提案アルゴリズムのある種の最適性を示した。なお、この研究はNECとの共同研究である。