湊離散構造処理系プロジェクト

 トップに戻る

プロジェクトホームページ

minato_portrait 研究総括　湊 真一
（北海道大学 大学院情報科学研究科　教授）
研究期間：2009年～2014年

 

 

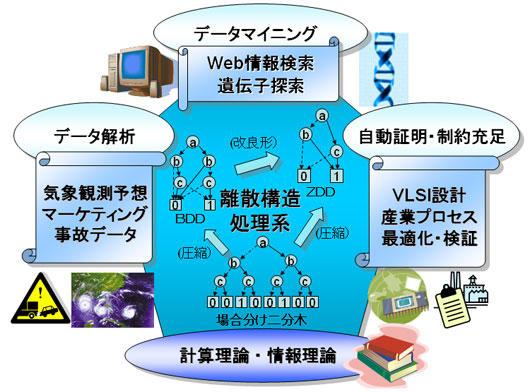
計算機は、産業プロセスの最適化や解析、マーケティング、バイオインフォマティクスなど、様々な情報処理に活用されています。近年の爆発的に増大している大規模データを処理するためには、計算機ハードウェアの高速化だけでなく、膨大な離散構造データ（計算機が行う論理的な処理を表現したデータ）を数学的に簡約化し効率よく計算する「アルゴリズム技術」の重要性が高まっています。本研究領域では、基本的な離散構造の１つである論理関数を処理するBDD（Binary Decision Diagram:二分決定グラフ）と、さらにその進化形であるZDD (Zero-Suppressed BDD; ゼロサプレス型BDD）の２つの技法を基盤とした離散構造処理系の研究に取り組んできました。ZDDは、研究総括が独自に考案したBDDの進化形で、疎な組合せの集合を効率よく処理する技法として世界的にも注目されています。今後もこれらの技法をさらに発展させ、多様な離散構造を統合的に演算処理する技法を体系化し、システム検証や最適化、データマイニング、知識発見などを含む分野横断的かつ大規模な実問題を高速に処理するための技術基盤を追究していきます。

fig1

研究成果

（１）ZDDを用いた配電網の網羅的解析に成功

当プロジェクトで開発されたフロンティア法（トップダウンに効率的に ZDDを構築していく手法）をもとに、配電網の効率的な解析技術の開発に取り組み、変電所設備72ヶ所，スイッチ数468個からなる実用的規模の配電網の構成において、天文学的に膨大なスイッチ構成（ON/OFF）の組合せを網羅的に列挙することに世界で初めて成功しました。また、与えられた電力品質条件を満たしつつ、かつ送電損失を最小化する最適構成を得ることに成功しました。配電網の組み合わせの総数はおよそ10の140乗に及びますが、制約を満たす構成は約10の63乗（割合ではわずか10の78乗分の１）であることを示し、これらの構成数を正確に算出することに成功しています。構成数の算出は市販PCでも数十分で計算可能で、ZDDの節点数（メモリ量）は約110万個（779MB、CD-ROM1枚分）でした。配電網の最適化や安定化の問題は、社会経済に与える影響が極めて大きく、潜在的な波及効果が極めて大きい研究成果です。さらにフロンティア法によるZDD構築は、配電網だけでなく、水道、ガス、鉄道、道路、通信、避難所配置、選挙区割りなど、様々な社会インフラの解析に応用できることから今後の活用が期待されています。

  1. Takeru Inoue, Keiji Takano, Takayuki Watanabe, Jun Kawahara, Ryo Yoshinaka, Akihiro Kishimoto, Koji Tsuda, Shin-ichi Minato, and Yasuhiro Hayashi，"Distribution Loss Minimization with Guaranteed Error Bound", IEEE Transactions on Smart Grid, Oct. 2013
  2. Takeru Inoue, Hiroaki Iwashita, Jun Kawahara, and Shin-ichi Minato, "Graphillion: ZDD-based Software Library for Very Large Sets of Graphs", The 18th Workshop on Synthesis And System Integration of Mixed Information technologies (SASIMI 2013), Sapporo, 2013
  3. 湊真一, "[招待講演] フロンティア法：BDD/ZDDを用いた高速なグラフ列挙索引化の技法", 電子情報通信学会情報ネットワーク研究会, 2012年8月
  4. Takeru Inoue, Norihito Yasuda, Shunsuke Kawano, Yuji Takenobu, Shin-ichi Minato, and Yasuhiro Hayashi "Distribution Network Verification for Secure Restoration by Enumerating All Critical Failures", IEEE Trans. Smart Grid, Vol. 6, No. 2, pp. 843-852 , Mar. 2015

 

fig2

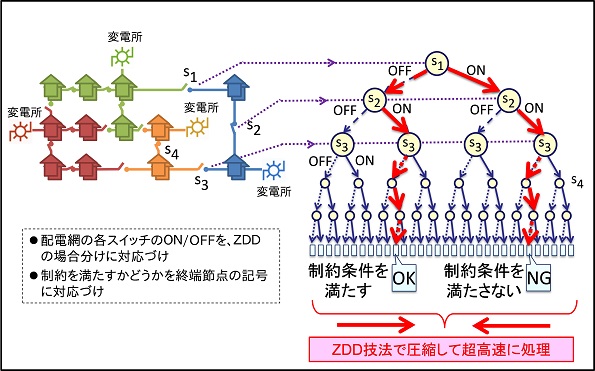
ZDDによるスマートグリッド配電網のモデル化

 

（２）ビッグデータから新たな科学的発見をもたらす統計手法

自然科学分野の研究において、新しい現象を見つけたときには、その結果の信頼性を統計的に担保する必要があり、誤発見の確率を示す検定値（P値）が広く用いられてきました。一般に観測できる対象（例：DNA変異）が増えると、誤発見の確率も高くなりますが、一般的な多重検定法では、P値に大きな補正係数を掛けて（補正P値）、それでも0.05以下の場合のみ発見とみなします。最もよく用いられるボンフェローニ法では、n個の対象がある場合、P値にnを掛けて補正しますが、逆に、データの観測対象が増えるとともに、科学的発見が減るという「ビッグデータのパラドックス」が起きる場合があり、自然科学分野においても観測データが膨大化しつつある近年では、極めて重大な課題となっています。本研究では、出現頻度が十分に低い組合せは誤発見率を変化させないという数理的性質に注目し、従来よりも格段に正確な補正 P 値を計算できるアルゴリズムLAMP（Limitless-Arity Multiple testing Procedure、無限次数多重検定法）を開発しました。本手法では、超高速アルゴリズムを用いて出現頻度が十分に低い組合せを特定し取り除くことによって、補正係数を大幅に削減することが可能です。本成果は、広く自然科学分野における科学的発見に寄与する成果であり、遺伝解析をはじめとした薬剤の創薬の他、社会科学分野の実験評価にも大きな影響を及ぼすことが期待されます。

  1. Aika Terada, Mariko Okada-Hatakeyama, Koji Tsuda, Jun Sese, "Statistical significance of combinatorial regulations", Proceedings of the National Academy of Sciences (PNAS), vol. 110 no. 32, August 2013
  2. Shin-ichi Minato, Takeaki Uno, Koji Tsuda, Aika Terada, and Jun Sese: "A Fast Method of Statistical Assessment for Combinatorial Hypotheses Based on Frequent Itemset Enumeration," In Proc. of The European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases 2014 (ECML PKDD 2014), Part II, (LNAI 8725, Springer), pp. 422-436, Sep. 2014

fig3

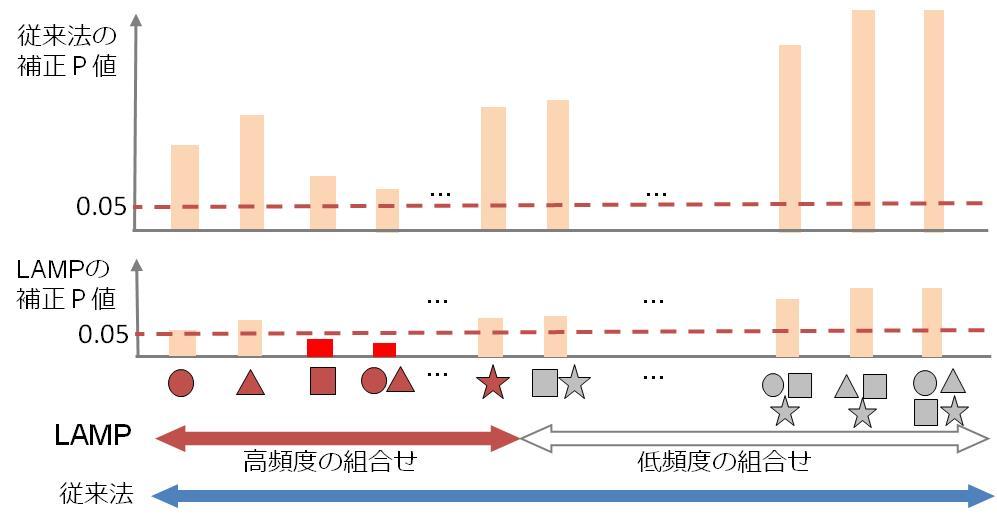
LAMPによる組み合わせ因子発見

 

（３）「フカシギの数え方」の展示と数え上げ世界記録

日本科学未来館のメディアラボ第11期展示として、湊プロジェクトの成果展示を行いました。「フカシギの数え方」と題した本展示は予想外の反響があり、2012年8月1日から2013年4月15日までの期間中、23万人を超える来場者数となり、小中高校生の他、大人にも十分楽しんでもらえる展示内容でした。また、展示コンテンツとして作成した「フカシギの数え方」のアニメ動画はYouTube上で170万アクセスを超えるヒットとなりました。「アルゴリズム技術」に関しては、従来なかなか一般人に理解してもらえるようなコンテンツはありませんでしたが、本展示で開発したコンテンツはその意味でも画期的なものだったと評価できます。YouTube動画に対しては海外からのコメントも数多く寄せられており、国際的にも日本の技術をアピールできたものと評価できます。2015年秋には、動画の名場面を集めたLINEスタンプ（未来館初のLINEスタンプ）を公開、巨大数表を印刷したクリアファイルを商品化して未来館ショップで発売する等、本研究成果のさらなるアウトリーチに努めました。本展示での格子グラフの数え上げ問題について、当プロジェクトは2013年11月にn=26（26×26の格子グラフ上のパス列挙）の数え上げに成功し、この問題の世界記録を更新しています。（https://oeis.org/A007764）。本成果は、アルゴリズム技術の面白さと社会的重要性をわかりやすく示したものであり、青少年や一般市民への波及効果は大きく、情報科学分野の将来の発展に大きく寄与するものと考えられます。

  1. 湊 真一(編), ERATO 湊離散構造処理系プロジェクト(著): “超高速グラフ列挙アルゴリズム－〈フカシギの数え方〉が 拓く，組合せ問題への新アプローチ－,” ISBN: 978-4627852617, 森北出版, Apr. 2015
  2. Hiroaki Iwashita, Yoshio Nakazawa, Jun Kawahara, Takeaki Uno, Shin-ichi Minato, "Fast Computation of the Number of Paths in a Grid Graph", The 16th Japan Conference on Discrete and Computational Geometry and Graphs (JCDCG2 2013), Tokyo
  3. 湊真一, "フカシギの不思議", 日本科学未来館 第11期メディアラボ トークイベント, 日本科学館, 2013/01/19
  4. 湊真一, "「おねえさんの問題」の最先端 ― YouTube動画と世界記録 ―", 情報処理, Vol. 54, No.11, pp. 1152-1159, Oct. 2013

fig4

未来館展示「フカシギの数え方」

 

fig5

YouTubeアニメ動画

 

 

評価・追跡調査

プログラム

  • CREST
  • さきがけ
  • ACT-X
  • ERATO
  • ALCA
  • CRONOS
  • AIPネットワークラボ
  • 終了事業アーカイブズ
  • ご意見・ご要望