成果概要
大規模自由度場のアクチュエータ位置最適化[2] アクチュエータ位置最適化の数理問題の定式化
2024年度までの進捗状況
1. 概要
気象場を効率的に変動させるようなアクチュエータ位置を求めるために、アクチュエータ位置最適化問題を定式化しました。評価指標を明確にすることでアクチュエータ配置の良し悪しを定量的に評価できるようになり、それに基づいてアクチュエータ配置を最適に決定するアルゴリズムの開発が可能となります。定式化された数理問題が複雑すぎると、大規模自由度場である気象場に対するアクチュエータ配置問題に解を与えることが困難となるため、アルゴリズム開発のテーマと協調しながら、数値解法の開発が可能な程度には簡便な数理問題を検討してきました。
2. これまでの主な成果
(1)線形時不変システムに対するアクチュエータ位置最適化問題の解析
線形時不変システムにおけるアクチュエータ位置最適化問題について検討してきました。ここでは、検討事項の一つである、可到達性グラミアンとリッカチ方程式の解を用いたアクチュエータ位置の評価指標に関する成果を紹介します。
線形時不変システム(図1上段)に対して、有限な二次制御制約規範のもとでの可到達集合を考えます。可到達集合の大きさはシステムの制御のしやすさを表すため、アクチュエータ位置の評価指標に利用できます。我々は、この可到達集合は状態空間における楕円体(図1中段)であり、その大きさが、あるリッカチ方程式の解である行列の大きさによって決まることを明らかにしました。また、状態に対する重み行列をゼロ行列とすると、このリッカチ方程式の解の逆行列が可到達性グラミアンに一致することを示すことができます。 したがって、リッカチ方程式の解の評価指標が可到達性グラミアンの解の評価指標の自然な拡張であるとみなせます。また、状態の重み行列が十分に小さいときは、二つの解の評価指標がほぼ等しくなる可能性が示唆されます。この場合、可到達性グラミアンの評価指標のほうが計算コストが低いため、リッカチ方程式の解の評価指標の代わりに、可到達性グラミアンの評価指標を利用したほうが効率が良いと考えられます。なお、リッカチ方程式の解やグラミアンなどの行列の大きさを測る尺度はいくつかありますが、それらの大小関係は不等式で表すことができます。

(2)非線形システムのためのアクチュエータ位置最適化問題の定式化
線形時不変システムにおける解析で得られた知見を活かし、気象場のような非線形システムのためのアクチュエータ位置最適化問題の定式化をしてきました。
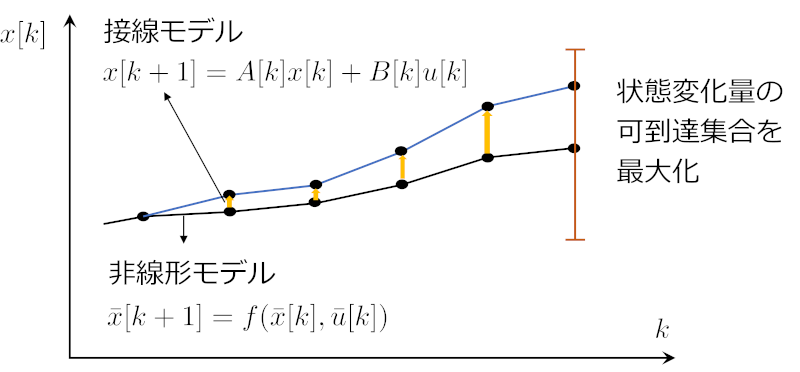
非線形システムにおいて制御介入によって発生した擾乱が十分小さければ、擾乱の時間発展は線形時変システムである接線形システムによって記述されます。そこで、接線形システムにしたがう擾乱が大きく変化するようなアクチュエータ位置を求める最適化問題を定式化しました。この問題では、制御入力の時系列から擾乱の時系列を出力するような感度行列(図2)に着目します。この感度行列から生成されるグラミアンの大きさを評価指標に使用します。このグラミアンの大きさは線形時不変システムにおけるいくつかの指標と関連があります。例えば、グラミアンの最大固有値と対角和は、それぞれ、線形時不変システムにおけるH∞ノルムとH2ノルムに似た指標となります。
上記の最適化問題では、低次元化手法と組み合わせることで、気象場のような大規模なシステムに対しても現実的な計算時間で良好な解を求めることができます。