Progress Report
Actuator Location Optimization for Large Degree-of-Freedom Fields[2] Mathematical Problem Formulation for Actuator Location Optimization
Progress until FY2024
1. Outline of the project
Actuator-position optimization problems have been formulated to find actuator positions that efficiently change states such as the temperature and the velocity of the atmosphere. By clarifying the evaluation metrics, it becomes possible to quantitatively evaluate the effect of the actuator placement and to develop an algorithm to determine the actuator placement. If the formulated mathematical problem is too complex, the problem cannot be solved. Hence, we have formulated the problems that are simple enough to solve, in coordination with the other themes.
2. Outcome so far
(1) Analysis of actuator-position optimization problems for linear time-invariant systems
We have studied actuator-position optimization problems in linear time-invariant (LTI) systems. Here, we present one of the results, a performance index for actuator positions using the reachability Gramian and the solutions of a Riccati equation.
We consider a reachable set under a finite quadratic control performance index for the LTI system (Figure 1). The size of the reachable set represents the controllability of the system and can be used as an indicator to evaluate the actuator positions. We found that the reachable set is an ellipsoid in the state space (middle of Fig. 1), and its size is determined by the size of the matrix that is the solution of a Riccati equation. We can also show that if the weight matrix for the state is a zero matrix, then the inverse matrix of the solution of the Riccati equation coincides with the reachability Gramian. Thus, we can consider the performance index of the solution of the Riccati equation to be a natural extension of the performance index of the reachability Gramian. It is also suggested that when the state weight matrix is sufficiently small, the two indices may be approximately equal. In this case, since the index of the reachability Gramian is less computationally expensive, it is more efficient to use this index instead of the index of the solution of the Riccati equation.

(2) Formulation of actuator-position optimization problems for nonlinear systems
We have used the knowledge gained from our analysis in LIT systems and formulated actuator-position optimization problems for nonlinear systems such as weather fields.
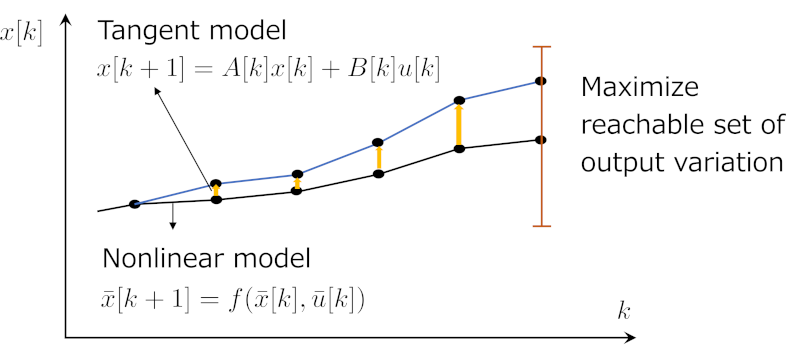
If the disturbance generated by a control intervention in a nonlinear system is sufficiently small, the time evolution of the disturbance can be described by a linear tangent system, which is a linear time-variant system. We formulated an optimization problem to find the actuator position such that the disturbances in linear tangent systems vary significantly. The problem based on linear systems yields a actuator placement algorithm with low computational complexity.
The problem focuses on a sensitivity matrix (Figure 2) which outputs the time series of the disturbances from the time series of the control inputs. The size of the Gramian generated from this sensitivity matrix is used as performance indices for actuator positions. The size of the Gramian is related to several indices for LTI systems. For example, the maximum eigenvalue and the trace of the Gramian are similar to the H∞ norm and the H2 norm in LTI systems, respectively.