Progress Report
Actuator Location Optimization for Large Degree-of-Freedom Fields[1] Development of Actuator Location Optimization Algorithm and Its Application to Modeling and Weather Problems
Progress until FY2024
1. Outline of the project
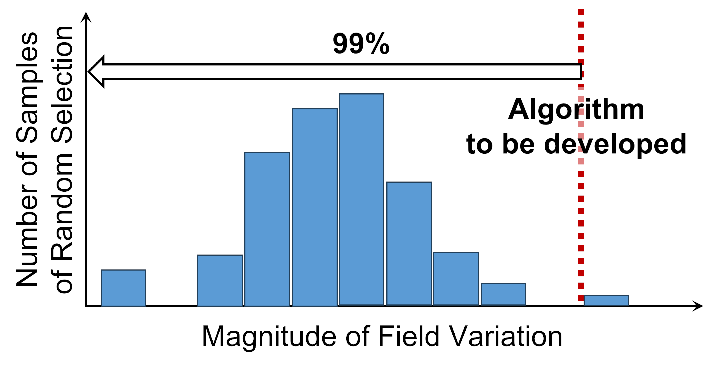
Since a weather field has a large number of degrees of freedom, weather simulations take quite a long time. Therefore, it is not practical to use an algorithm that performs a huge number of weather simulations for actuator selection. We develop actuator-position-selection algorithms that can be applied to such large systems based on a mathematically formulated problem in this theme. To efficiently evaluate the performance of the algorithm, simulation models of relatively small systems are also developed in parallel with the development of the actuator-selection algorithm. For these test models, the developed algorithm shows that the actuation at the selected location can significantly modify the field with a probability of over 99% better than that at a randomly selected location (Fig.1). We finally show the effectivity of the developed algorithm for a weather model.
2. Outcome so far
We have developed some numerical algorithms to optimize actuator placement in a linear model by considering the dual problem of sensor placement optimization. Further, we have evaluated their efficiency not only with small-scale problems but also with large scale problems including weather fields.
First, we proposed an algorithm for time-invariant linear model with impulse forcing. In this algorithm the determinant of a matrix associated with right singular vectors is maximized by greedy method. This algorithm was applied to a linearized Ginzburg-Landau model and it was shown that the system can produce an output with various modes (Fig. 2). Further, it was indicated that the algorithm can be applied to a large-scale system such as compressible axisymmetric jets when randomized singular value decomposition is used.
Then, we developed an optimization algorithm for a time-variant linear system, which may be considered as a perturbation system of a nonlinear system such as meteorological phenomena.
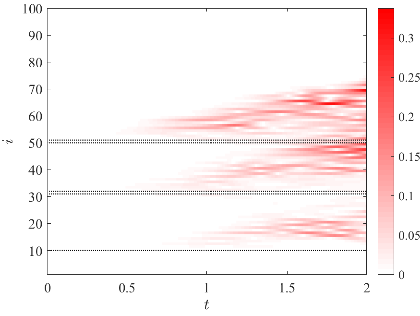
In this algorithm actuators are placed so that the reach set of the time- series output is maximized. We applied this algorithm to Lorenz-96 model, which is known as a simple model of meteorological phenomena, and numerically showed that the model can be controlled efficiently (Fig. 3)

Further, we developed an algorithm for randomized singular vector method by using a weather simulator called WRF (Weather Research & Forecasting Model) and optimized actuator locations in a weather field. It is numerically shown that the weather field could be varied more efficiently with optimized actuators than by those placed randomly or placed according to our intuition (Fig. 4-7).



