One of the hardware challenges in realizing a fault-tolerant universal quantum computer is that a large number of physical qubits are required to implement error-correcting codes, and in the case of superconducting qubits, the number is said to be as many as 10⁸ with a typical error rate of 0.1%.
In this research and development theme, to solve this problem, we aim to improve the coherence time of the qubits, develop manufacturing technology of high-quality quantum bits to reduce the error rate, and contribute to reducing the number of quantum bits needed for the realization of fault-tolerant universal quantum computers. In addition, we will develop quantum bit manufacturing technology using optical lithography and multi-layer processes in order to improve the productivity and the uniformity of quantum bits for future large-scale circuits.
We will also conduct exploratory research on bosonic codes, which are expected to enable fault-tolerant quantum computation with fewer physical qubits than those required in the current mainstream of the surface code, to identify their possibilities and promising schemes.

① Development of high-coherence superconducting qubits

Recent studies revealed that dielectric loss at the interface layers such as that between the substrate and the superconducting metal is one of the main sources of decoherence in the superconducting qubits. We try to realize high-quality Nb-based transmon qubits through the optimization of the fabrication processes, particularly paying attention to those interfaces. By clarifying the fabrication process which has large impact on the qubit lifetime (T₁), we aim to establish the fabrication recipe to produce high-quality qubits in a reproducible way.
By using Nb electrode for the capacitor and Al-based Josephson junctions on the Si substrate, we have achieved maximum averaged T₁ of ~170 us, which corresponds to the quality factor of 5M (left figure below). By measuring the T₁ of several transmon qubits with different design of the capacitor pads, we found that the dielectric loss at the interfaces is still limiting the T₁ of those qubits (right figure below).

② Research and development of bosonic cords using superconducting resonators

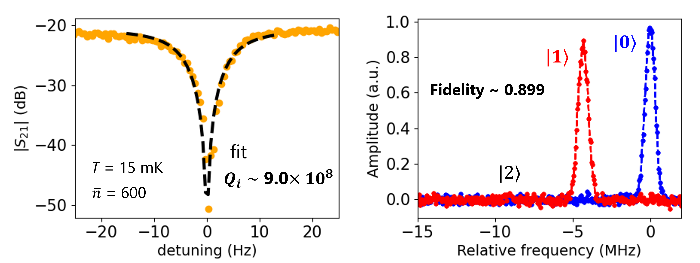
Error-correcting codes, known as bosonic codes, are a method for protecting quantum information from errors by utilizing the degrees of freedom found in the energy levels of resonators. Because these energy levels are theoretically infinite, bosonic code can potentially reduce the number of physical qubits required compared to conventional error-correcting codes. In our efforts to improve the Q factor of a three-dimensional resonator (cavity) made of niobium, which is a key component of a bosonic qubit, we improved surface treatment of the cavity. This advancement led to a Q factor exceeding 10⁹, achieving one of the highest levels in the world, with good reproducibility. Furthermore, we constructed a bosonic qubit composed of a three-dimensional resonator for memory, an ancilla qubit, and a readout resonator, and successfully encoded the logical states, | 0_L 〉, | 1_L 〉 of binomial (1,1) code using optimized control pulses. A pseudo-fidelity of over 90% was achieved in this experiment.