Harmony of Gröbner bases and the modern industrial society

Applied Mathematics Group

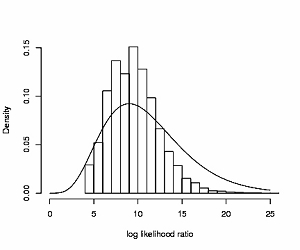
Computational algebraic statistics is an attractive and rapidly developing field. In this field, statistical models are characterized as a subset of the solutions of polynomial equations and are analyzed by algebraic tools based on the theory of Gröbner bases. For example, in the analysis of contingency tables, Gröbner basis plays a fundamental role for calculating P-values of various exact tests. Precisely, Gröbner basis relates to a generator of a connected Markov chain over the discrete sample space with the given marginal totals. After this discovery, the theory of calculating P-values of exact tests has been rapidly developed, which enables us to obtain sufficiently accurate P-values for data sets with small sample sizes and not to rely on the classical large sample theory. However, in the real statistical applications where complicated models or data of large size are treated, algebraic computation for them becomes also complicated and infeasible. We investigate the structure of Gröbner basis for the important statistical models in the real world from the viewpoints of theory and computation.

This figure is an example of Markov basis elements for the three -way contingency tables. Markov basis consists of a set of elements of such types. In the real applications, Markov basis includes elements of higher orders, which have complicated structures.

This figure illustrates the difference of an asymptotic distribution (smooth line) by large sample theory and a Monte Carlo estimated exact distribution (histogram) obtained from the algebraic statistical approach. When the fitting of large sample theory is poor like this example, the algebraic statistical approach is valuable.