事業成果
機械学習の分類性能の向上はどこまで続く?
機械学習の最良性能を推定する技術の研究2024年度更新

- 石田 隆(理化学研究所 革新知能統合研究センター 研究員/東京大学 大学院新領域創成科学研究科 講師)
- ACT-X
- 「数理・情報のフロンティア」領域・「ベイズ誤差推定及び正則化手法の研究」研究者(2020-2022)
適切に機械学習データを評価するベイズ誤差推定手法を提案
機械学習のためにはどのようなデータをどのくらいの量収集・学習すればよいのかの判断が、精度とコストに直結する。その判断基準として重要なのがベイズ誤差※1の推定である。
ベイズ誤差の推定法の研究はこれまで特殊なケースでしか行われていなかったが、理化学研究所研究員・東京大学講師の石田隆氏はさまざまな分類問題で活用可能なベイズ誤差推定技術を研究している。その研究から分類問題における新しいベイズ誤差推定手法を導き出し、提案した手法は機械学習・深層学習の国際会議ICLR 2023にNotable top 5%(注目のトップ5%)として採択された。
その一方、過学習を防ぐための「正則化」の手法も研究対象だ。これについては、ベイズ誤差推定値をもとに正則化のためのハイパーパラメータ(学習前に人間が設定する各種の値)のチューニングに活用可能と考えられており、分類器の新しい学習手法やニューラルネットの正則化手法についても研究中だ。
なお、ベイズ誤差の研究とは別に、ハードラベル※2が与えられた状況での正則化手法の研究プロジェクトにも携わり、その提案手法は、IEEE(米国電気電子学会、エレクトロニクス関係で世界最大の学会)の Transactions on Pattern Analysis and Machine Intelligenceに採択されている。
※1 ベイズ誤差
分類問題における予測誤差の下限。最良性能の指標として活用することができる。
※2 ソフトラベル/ハードラベル
教師あり学習の学習データの答の部分の正/負がはっきりしているものをハードラベル、どちらとも言い切れず、割合で示されるものをソフトラベルと呼ぶ。
学習すべきデータセットの適切な質や量を見いだすために
AI活用の基礎になる機械学習において、どのようなデータセットを学習させるかは極めて重要なファクターだ。一般的にはデータが少なくて質が悪いと推測の精度が低くなり、適切な量で良質なデータを学習すれば精度が高くなる。しかし良質であってもデータの学習量が多すぎると「過学習」といってかえって精度が低くなることもある。また目的やデータの性格によってはそもそも機械学習に向かない場合もある。どれだけデータを収集して学習させるのが適切なのかの判断は難問だが、基本的な判断材料として、ベイズ誤差の推定値を利用する方法がある。
教師あり学習※3におけるベイズ誤差とは、与えられた問題に対する予測誤差の下限を指す。ベイズ誤差を推定する技術が発達すれば、扱いたいデータ分析の問題に対して、その限界性能をあらかじめ知ることができる。その限界性能が目的にふさわしいかどうかで分析プロジェクトの可否を事前に判断でき、また適切な性能になるようにデータを追加する判断や、過学習にならないように早期に学習を停止する判断も可能になるだろう。すなわち、機械学習モデルの訓練に対して、定量的な目標設定ができることになる。
また、さまざまなデータセットについてベイズ誤差を推定することができれば、それに応じて正則化の強さのチューニングに活用できるなど、さらに大きく可能性が広がる。
※3 教師あり学習
機械学習の分野の1つで、事前に入力インスタンスとラベルの組を大量に作成して学習を行う。
データ収集コストを制限しても正しいベイズ誤差を推定可能に
ベイズ誤差推定の研究では、インスタンス(入力データ点)に対する事後確率のうち、最大の値になるクラスの値を直接収集するだけでベイズ誤差が推定できる手法を開発したのが大きなポイントだ。事後確率が最大となるクラスの事後確率の情報さえあれば、インスタンスは必要ない。
つまり、インスタンスを収集しないことでコストを抑えたり、データ収集の制約があったりする状況でも、ベイズ誤差推定が実施可能になる。もちろんインスタンスがすでにある場合でもこの手法は利用できる。
なお、特定の雑音付きのソフトラベル※2(教師データの答が正/負の1,0でなく0.5や0.75のようなもっともらしさの割合になるような値)が収集できる場合や、複数のハードラベルが収集できる場合などのより現実的な設定であっても、一致性や不偏性、もしくは漸近不偏性などの優れた統計的性質をもつ。
人工データを用いた実験では、「ソフトラベルが与えられる場合」「雑音付きのソフトラベルが与えられる場合」「正信頼度が与えられる場合」の各場合において、真のベイズ誤差を正確に推定できることを確認している。例えば図1では、非常に少ないデータ数でも正確に推定できることを確認できる。
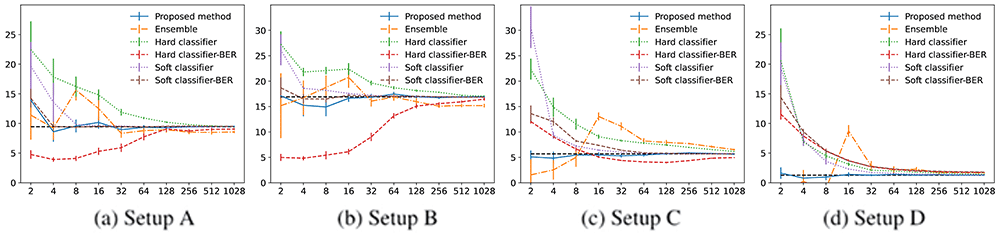
図1 ソフトラベルが与えられる場合の人工データ実験の結果
データ数を増やしていくと、新手法で推定した値(青)が真のベイズ誤差(黒の点線)に近づいていくことがわかる。
また、機械学習で頻繁に用いられるベンチマークデータセットなどの実データを対象にベイズ誤差を推定した。最近のモデルを用いた場合の性能は、ベイズ誤差推定値と同等レベルであることから、これらのデータセットではすでに限界性能に達している可能性を示した。他にも、ベイズ誤差を用いて学術的な国際会議の難易度を推定するという応用例にも取り組んだ。
正則化手法については、ソフトラベルを用いて分類器を学習する新たな手法の研究を進めているほか、ニューラルネットワークの正則化手法に取り組み、独自の正則化手法を提案している。
多様な指標の限界性能推定手法に挑戦
上記のように、二値分類におけるベイズ誤差を推定する手法について提案が実現したが、今後はさらに対象を広げていく。すでに他研究グループが今回の手法を多値分類におけるベイズ誤差に発展させることや特定の問題への適用が発表されるなど、広がりを見せているが、他にもさまざまな指標を対象に限界性能を推定することなどが研究対象になる。
- 情報通信の成果一覧へ
- 事業成果Topへ
- English