About ERATO MMSD Project

ERATO MMSD Project

New! A position paper about the project has been published.

ERATO MMSD is a JST-funded 5.5-year research project (via the ERATO funding scheme), dedicated to Metamathematics for Systems Design. The project director is Ichiro Hasuo.

This broad project aims to extend the realm of formal methods from software to cyber-physical systems (CPS) and manufacturing - automotive industry in particular. The extended methods, for goals including specification, verification and synthesis, should address key additional concerns in manufacturing, such as continuous dynamics and quantitative measures like probability and time. The project covers many different fields: formal methods, software science, software engineering, control theory, machine learning, optimization, and so on. Particular emphases are placed on:

metatheories on the theoretical side, expressed in mathematical languages like logic and category theory, to guide the process of extending (object-level theories of) formal methods; and
industrial application on the practical side, in which we collaborate with manufacturing companies and solve their specific problems. We hope that those successful applications, if rather small-scale, will eventually pave the way to the development of a large-scale software suite for comprehensive support of manufacturing with formal methods.

A large part of the project’s activities will be at our Tokyo site, in central Tokyo with convenient access. Our Tokyo site hosts

Group 0 (Metatheoretical Integration, led by Shin-ya Katsumata),
Group 1 (Heterogeneous Formal Methods, led by Ichiro Hasuo) and
Group 3 (Formal Methods and Intelligence, led by Fuyuki Ishikawa).

Another principal site is in Waterloo, Canada. This site hosts

Group 2 (Formal Methods in Industry, led by Krzysztof Czarnecki).

The team will be a vibrant and international one: we expect more than half of the staff to be from overseas. The working language is English.

Our Four Groups: Missions and Research Topics

Our research activities are centered around the extension scheme T + e -> T(e), where:

T is a formal methods technique (or "theory") that is originally for software, hence is discrete and qualitative;
e is an additional concern (such as continuous dynamics or a quantitative quality measure); and
T(e) is the technique/theory obtained by extending T with e.

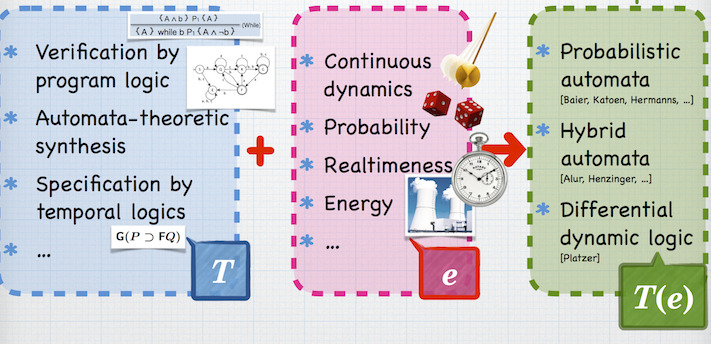
The project is organized into the following four groups.

Group 0: Metatheoretical Integration

The group, led by Shin-ya Katsumata, aims to formulate the extension processes T + e -> T(e) themselves in rigorous mathematical terms. Here T is an object-level theory; and a theory of extension processes T + e -> T(e) is hence a meta-level theory. Such a metatheory would allow the definition of T(e) - as well as its correctness results such as soundness - that applies uniformly to general T's and e's (under suitable conditions).

Relevant technical fields are mathematical logic and category theory as languages for describing mathematical theories. Specific examples of developments in this direction include the following.

In our nonstandard transfer research program, we exploit nonstandard analysis - as a fruit of model theory - to comprehensively transfer discrete verification techniques to continuous/hybrid dynamics. Here an (object-level) theory T is an arbitrary verification technique formulated in the first-order logic; and an additional concern e is continuous dynamics incorporated by means of a fresh constant dt. [Suenaga & Hasuo, ICALP'11; Hasuo & Suenaga, CAV'12; Suenaga, Sekine & Hasuo, POPL'13; Kido, Chaudhuri & Hasuo, VMCAI'16].
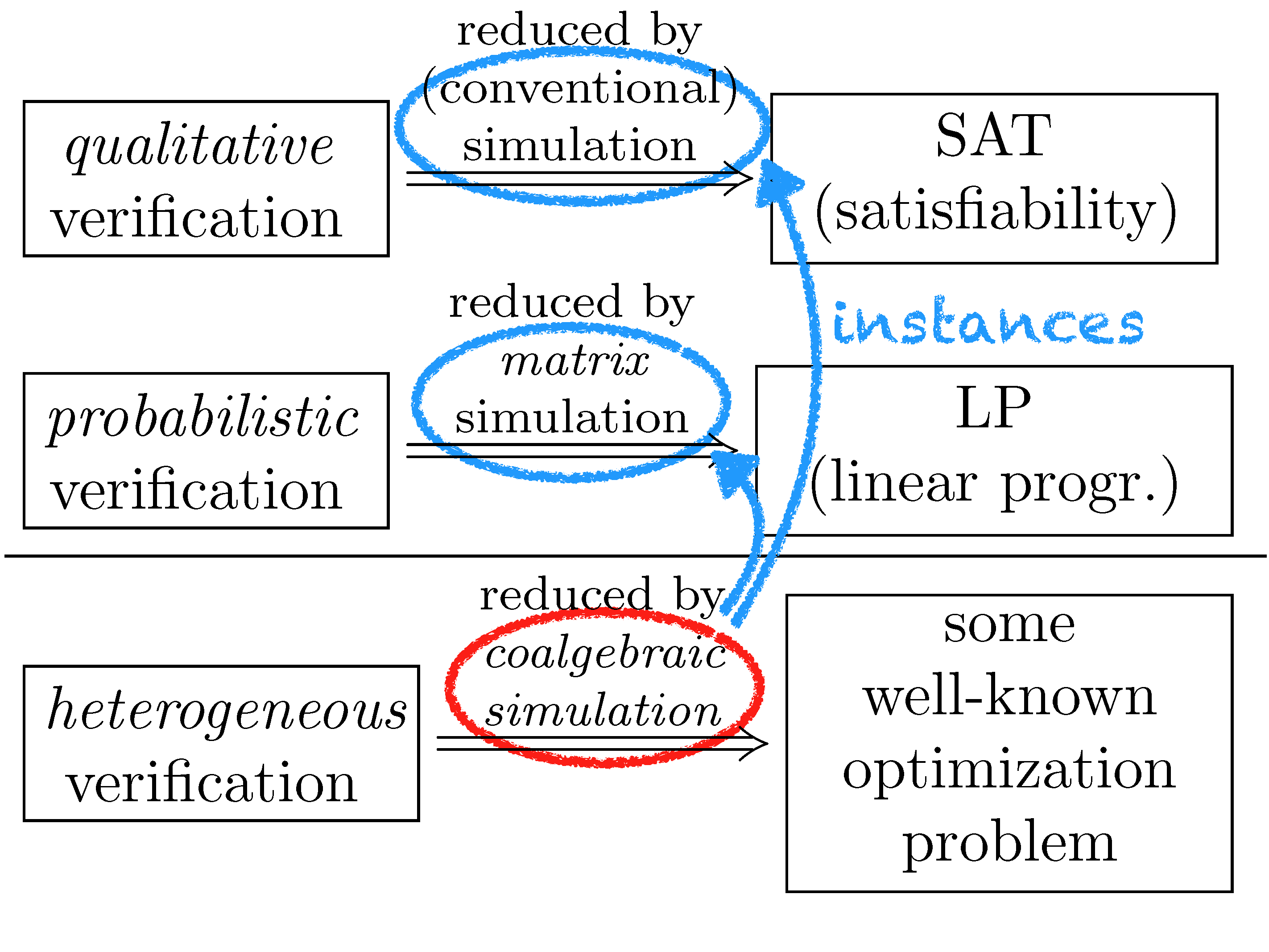
Coalgebraic unfolding. Many techniques in formal methods can be understood as those for reduction ("unfolding") of structurally complex verification problems to structurally simpler problems. The latter include SAT, graph reachability, LP and other optimization problems, for which efficient solvers have been studied and implemented. Depending on the nature of the original problem (e.g. qualitative vs. quantitative) the target problem will differ; however the reduction processes themselves often exhibit structural similarities.

With coalgebraic modeling - where the abstraction power of the categorical language is exploited - it becomes possible to rigorously formulate such similarities, and to describe and study seemingly-different reduction processes in a uniform manner. Here T consists of techniques from automata theory; and e is a notion of quantity, typically modeled by a semiring and a monad arising thereby. [Hasuo, Jacobs & Sokolova, LMCS'07; Hasuo, CONCUR'10; Urabe & Hasuo, CONCUR'14 & CALCO'15; Hasuo, Shimizu & Cirstea, POPL'16; Urabe, Shimizu & Hasuo, CONCUR'16].

Group 1: Heterogeneous Formal Methods

The mission of the group, led by Ichiro Hasuo, is to conduct the extension T + e -> T(e) for a variety of T's and e's. The extension will be guided by real-world applications as well as by our metatheories (i.e. general extension schemes); conversely developments in Group 1 will also provide concrete extensions T + e -> T(e) that will then inspire their matatheoretical unification by Group 0. Collaboration with control theory - a discipline that is complementary to software science in the study of CPS - will be a key aspect of the group activities.

Potential concrete research topics include, but are not restricted to, the following.

Unification of formal methods and control theory centered around temporal logics as specification formalisms, as is exemplified by the well-known correspondences between: ranking functions and Lyapunov functions; and invariants and barrier certificates. Also relevant here is quantitative logics in which truth is not two-valued but continuous. Examples of such logics include: temporal logics with robustness semantics (see e.g. [Fainekos & Pappas, Theor. Comp. Sci.’09; Akazaki & Hasuo, CAV'15]); and those with discounting (see e.g. [Nakagawa & Hasuo, TGC'15]).
Dealing with continuous state spaces - that pose fundamental challenges to many formal methods techniques that are inherently combinatorial and finitary. One way of doing so is to discretize a continuous state space into a finite one, e.g. via a approximate bisimulation [Girard & Pappas, Eur. J. Contr. '11]. Aside from these automata-like representations, there are many other possible symbolic representations. Among them are polynomials, in the analysis of which real algebraic geometry (see e.g. [Bochnak, Coste & Roy, '98]) plays an important role.

Group 2: Formal Methods in Industry

This group is led by Krzysztof Czarnecki who has software engineering backgrounds. It is based in Waterloo, Canada where a number of strategic initiatives are taking place towards collaborations with automotive industry (such as WatCAR and Autonomoose). The group's mission is to pursue effectiveness of the theories and techniques developed in the project (especially by Groups 1 and 3). It applies the techniques to real-world applications and at the same time identifies key theoretical challenges that are then fed back to the other groups. Of particular interests are the following topics.

Formalization of models and specifications that are often given informally in design processes in industry. Asking engineers to learn and write using formal specification languages is one possible way but not the only one. We seek (semi-)automation of formalization processes employing (ideas and/or techniques from) formal methods. We envisage a tool that: asks engineers questions that they can easily answer; learns a formal model/specification from those answers; and shows some cornerstone trajectories to be further inspected by engineers.
A topic closely related is user interface. (Some of) our tools are expected to work closely with engineers that have domain knowledge but are not necessarily comfortable with formal methods. To be able to exploit engineers' domain expertise the tools' ease of use is essential; so is the quality and accessibility of feedbacks provided by the tools (formal proofs are not often appreciated by engineers, for example).

Group 3: Formal Methods and Intelligence

Many problems in cyber-physical systems are inherently out of the reach of conventional automated formal methods techniques - as is witnessed by the fact that reachability is undecidable for hybrid automata. Dealing with systems as complex as cars today is also cursed by dimensions and prohibits techniques that rely on exhaustive search. A common way around is interactive theorem proving, but it would require vast human cost and is thus unrealistic in many industry scenarios. We will therefore pursue two kinds of "intelligence" that would guide formal methods techniques (especially searches therein).

One is machine learning (ML) and artificial intelligence (AI) whose significance is growing nowadays in every academic, industrial and social field. An example of collaboration between formal methods and ML/AI is falsification (see e.g. [Fainekos & Pappas, Theor. Comp. Sci.’09; Akazaki & Hasuo, CAV'15]) where robust semantics of temporal logic gives characteristics based on which erroneous input is guessed. Conversely formal methods are expected to complement ML/AI, too, in dependability assurance that is critical in CPS applications.

Another kind of "intelligence" that we aim to exploit is human intelligence that creates knowledge indispensable for effective engineering activities. Firstly, intensive investigation and exploitation of domain knowledge is vital in CPS engineering as CPS involve various application domains and face rapidly changing environments. Secondly, engineering knowledge, including so-called heuristics and patterns, is the key for efficient methods to cope with search spaces that are too large to explore. Here user interface is essential in working successfully with human intelligence, i.e., with domain experts, engineers, and end users. From the viewpoint of theoretical studies of formal methods: most techniques assume as their users either computer science PhDs (for interactive theorem proving) or just anybody (for automated algorithms). We will seek the third way in which a tool learns from engineers' "intelligence" without requiring their fluency in formal specification/modeling languages.

The group, led by Fuyuki Ishikawa, will pursue the collaboration between formal methods and such "intelligence." The group's goal is similar to that of Group 1 - namely extension T + e -> T(e) - but Group 3 approaches it principally via software engineering, ML/AI and user interface (while Group 1 is via software science and control theory).