Research Results
Substantially reducing the number of operations in computing
Development of super high-speed algorithms FY2017

- Shinichi Minato (Professor, Graduate School of Information Science and Technology, Hokkaido University)
- ERATO
- "MINATO Discrete Structure Processing System Project" Research Director (2009–2014)
Super high-speed enumeration of a vast amount of combinations
There is a unit called"mysterious"in Japan. It's the unit of the number 10 to the power of 64. Actually, we are sometimes faced with 10 to the power of 64 alternatives in exploring the best combinatorial solution, for example, transfer in a train network, or switching an electric power distribution network. What should be done to find the best solution by enumerating these combinations in a short time and low cost? A key technique to this question is the "algorithm," description of the computation procedure and strategies for processing.
Today, computers are used for processing information, including for optimization and analysis of industrial processes, marketing and bioinformatics. In recent years, we need to process explosively growing Big Data, and the importance of algorithmic techniques has been recognized more and more, as well as the hardware speed up. To contribute such problems, Professor Shin-ichi Minato, ERATO research director, has tackled the research of "discrete structure manipulation system," a state-of-the-art system for efficiently processing discrete structures (mathematical model represented by discrete symbols).
Reducing the number of operations in computing
The basis of this study is the Zero-suppressed BDD (ZDD) devised by Professor Minato in 1993 and attracting worldwide attention (Figure 1). Logic functions are one of the basic discrete structures. In general, a logic function can be expressed as a binary decision tree when we classify the results of the logic function for all possible patterns of the input variables. Replacing this by computer processing, the number of branches means the number of processing times. As a device to reduce the number of processing times, an algorithm using a data structure called a binary decision diagram (BDD) was contrived in the United States in 1986. The ZDD that Professor Minato devised evolves this BDD into processing of aggregated data and can substantially compress the number of processing times in a case where, for example, an extremely small number is selected from a vast population, like selecting 10 items from 10,000 products. Though it depends on the case, it is said that compression several tens to several hundreds of times higher than BDD can be achieved by using ZDD.
Figure 1
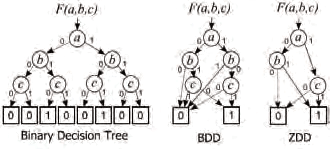
ZDD on the right is zero-suppressed BDD Professor Minato devised.
Succeeded in optimizing smart grid
Professor Minato et al. systematized a technique for comprehensively processing various discrete structures by developing the techniques of BDD and ZDD. They aimed at processing real cross-sector, large-scale problems, including system verification and optimization, data mining, and knowledge discovery. As one of their results, the development of a technique called the Frontier method and its application can be cited. The Frontier method is a technique that constructs ZDD and that enumerates all combinations that satisfy a constraint condition given in the form of a general graph structure, which has increasingly been applied to the analysis of various social infrastructures. As an example, analysis of a power network called a smart grid can be cited. They succeeded for the first time in the world in comprehensively enumerating and indexing astronomically many combinations of switch configurations (ON/OFF) in a typical electrical power network consisting of 72 substations and 468 switches and obtaining the optimum configuration that minimizes transmission loss while meeting the given electrical power conditions.
Development of software and publishing a technical guide
In ERATO, a study of path enumeration problems (Figure 2) of effectively counting the total number of paths between two diagonal points of an n × n grid graph without going through the same point more than once, though detouring is acceptable, was also conducted by using ZDD. In November 2013, the total number of paths in a case of n = 26 was successfully counted for the first time in the world. It took one week. If it were counted with a naive method, it is said that it would have taken 29 billion years even in the case of n = 11. The same problem, however, can be allegedly solved in several seconds by their algorithm.
Supplying the technique cultivated by the study in the form easy for researchers and industries to use is one of the objectives of Professor Minato. The research result of the path enumeration problem is supplied as Graphillion, a software for super high-speed graph enumeration and indexing. In addition, a technical book that describes how to use this software and summarizes the internal algorithm technique, Super High-speed Graph Enumeration Algorithm, was published in April 2015 (Morikita Publishing Co., Ltd.), rallying a lot of support and going through several editions. Moreover, an electoral district allocation analysis program based on the result of the study was also developed.
The result of ERATO is expected to be used widely because it can be used in the analysis of various social infrastructures, such as water services, gas, railroad, road, communication, and shelter installation, as well as smart grids and electoral district allocation.
Figure 2
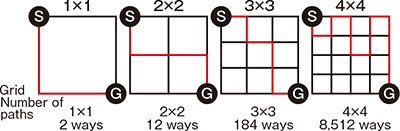
The total number of paths will explosively increase as the number of grids of a graph increases. It will be 1,282,816 ways in the case of 5 × 5 and as many as 575,780,564 ways in the case of 6 × 6.
"The Art of 1064 -Understanding Vastness-" Time with class! Let's count!
Video produced for exhibition at the National Museum of Emerging Science and Innovation (Miraikan)
![]() Played back 1.75 million times on YouTube (as of January 2016)
Played back 1.75 million times on YouTube (as of January 2016)
