Research Results
Accelerating social acceptance of self-driving technology
Mathematical approach guarantees ultimate safetyFY2023

- HASUO Ichiro (Professor of Information Systems Architecture Science Research Division, National Institute of Informatics)
- ERATO
- Research Director (2016-2024), "HASUO Metamathematics for Systems Design"
Mathematically proving the safety of self-driving
This research team is using its expertise in the abstract mathematical theory called "category theory"*1 to conduct various studies that will lead to improvements in the efficiency of processes and the quality of computer-equipped machines (cyber-physical systems), such as automobiles. It has achieved a wide range of applications, including simulations for extracting complex hazardous driving conditions for self-driving vehicles, and automatic improvement of the efficiency of gas turbine system design, which conventionally required the advanced know-how of experts.
The team has developed a new methodology to mathematically prove the safety of self-driving in the autonomous driving field. The development of self-driving software requires a vast array of driving scenarios concerning surrounding vehicles, pedestrians, etc., and the assessment of its safety. Existing proof methodologies, however, have been limited to simple driving scenarios, such as following a vehicle ahead on a road with no forks, for safety evaluation. In contrast, the researchers developed logical safety rules and proved their correctness for complex driving scenarios, such as coming to an emergency stop at a safe location while avoiding a collision with other vehicles.
*1 Category theory
A branch of mathematics that deals abstractly with mathematical structures and the relationships between them. Raising the level of abstraction of various theories allows us to grasp their common essence.
Safety of self-driving regarded difficult to prove
Self-driving car systems are bringing revolutionary changes to our lives towards a safe and secure society. In order to make them practical and accepted by society, it is necessary to guarantee a high level of safety and reliability, and explain them in a convincing way so that they will be accepted for driving on public roads. The current mainstream approaches to guaranteeing safety are "guarantee by statistical data of accidents" and "test by computer simulation", which are based on empiricism and statistics, still leaving the question of why it can be said to be sufficiently safe and how it can be explained to convince society. Therefore, a logical approach to the explanation of safety that is more reliable and easier to understand is strongly desired. Under these circumstances, some attempts to mathematically prove the safety of mechanical systems using "formal logic" have been made in the aeronautics and aerospace fields. However, they have rarely been applied to self-driving, which requires flexibility to handle various traffic situations.
Realizing safety assessments of complex driving scenarios
A methodology for guaranteeing the safety of self-driving vehicles called Responsibility-Sensitive Safety (RSS) (Fig. 1), proposed by researchers of statistical AI and automated driving, has been attracting attention in recent years. RSS aims to guarantee rigorous safety for self-driving vehicles by expressing driving rules in the form of explicit mathematical equations to achieve traffic safety, and by logically proving the validity of these equations. Logically proving safety using mathematics can be the ultimate form of guarantee, in terms of both the degree of guarantee, and the capability to explain the correctness of the conclusion (safety of self-driving vehicles) to society by clarifying the process by which it is proved.
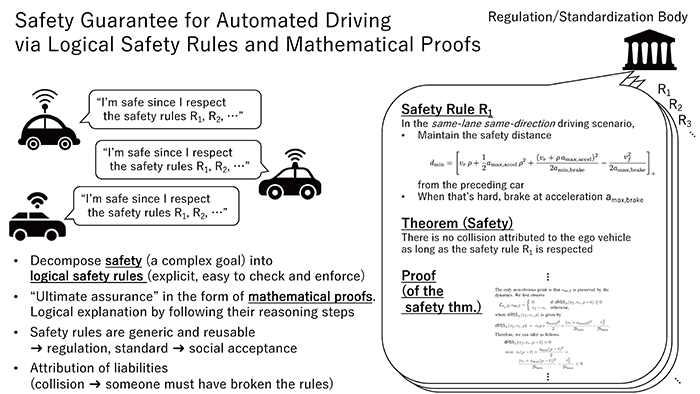
Fig. 1
Approach to self-driving safety based on a mathematical proof. The approach is shared by the method proposed in this study, "GA-RSS", and the original RSS. This approach proposes mathematically rigorous logical safety rules, and as a "safety theorem", also mathematically proves that "accidents will not occur as long as these logical safety rules are followed".
The "logical safety rules" established by RSS to be followed by self-driving vehicles are generic (independent of manufacturer, vehicle type, etc.), and can be used as international standards, industry standards or traffic regulations, thus they are expected to promote social acceptance of self-driving. However, the scope of the guarantee was limited to simple driving scenarios, such as following a vehicle ahead on a road with no forks.
The research team tried to overcome this limitation of the original RSS by establishing a new technical foundation, and proposed GA-RSS (Goal-Aware RSS), which is an extended version of RSS. A system of formal logic named differential Floyd-Hoare Logic (dFHL) was proposed to cater the extension to GA-RSS. Based on this, a derivation workflow and software support for new logical safety rules were designed and implemented (Fig. 2).
dFHL is a system of formal logic for efficiently proving the safety of hybrid systems*2 covering both digital and analog aspects, as in the case of automobile control realized by the collaboration of software and mechanics. It was devised as an extension of "Floyd-Hoare Logic", which was often used to verify the specifications of a software system. This new logic system, dFHL, makes it possible to sequentially analyze complex action plans for self-driving vehicles by dividing them into segments, thus extending the range of driving scenarios.
*2 Hybrid system
A dynamic system that has both the digital, discrete dynamics of a computer, and the analog, continuous dynamics of a physical system
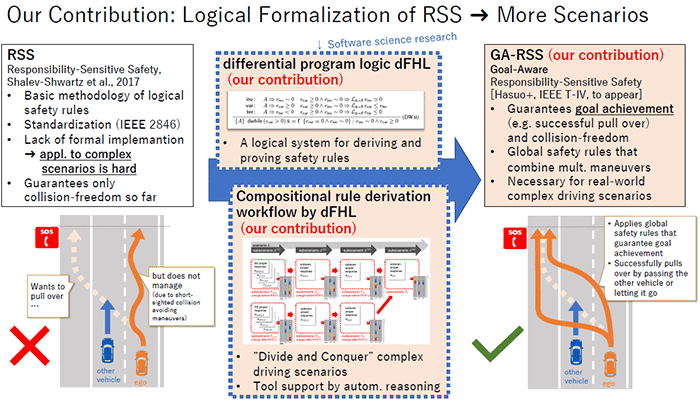
Fig. 2 Full-scale development of safety rules through the extension of RSS by formal logic
Combined with the differential program logic dFHL (middle block), RSS (left block) is extended to GA-RSS (right block), making it applicable to a wide variety of self-driving situations. In the example of an emergency stop shown in the figure, the original RSS safety rules enforce short-sighted collision avoidance behavior, so lane changes cannot be made when other vehicles are in the way, and the goal of emergency stop cannot be achieved. In contrast, in the proposed GA-RSS, a global action plan to avoid other vehicles by accelerating and braking can be incorporated into the safety rules, and the goal of an emergency stop can be achieved.
Giving impetus to social acceptance of self-driving
The application of RSS to automated vehicles is gaining momentum in the form of applications to actual products by multiple companies and discussions on international standards such as IEEE 2846. GA-RSS, the result of this research, extends the application of RSS from simple driving scenarios to realistic and complex ones consisting of multiple driving maneuvers, such as emergency stops, and it logically guarantees ultimate safety for those scenarios. This will contribute to dispel society’s concerns about the safety of automated driving, and provide a major impetus for the social acceptance of automated driving and the development of industries related to it. The rule derivation workflow and software support of safety assurance developed by the research team will enable logical safety rules for a complex driving scenario in a realistic timeframe of only a few weeks. Further, since the logical safety rules are highly versatile and independent of the manufacturer and vehicle type, they can be used for many years as an asset for society as a whole.
