Research Results
Contributing to policy-making with mathematical models
Predicting and controlling infectious diseases in near futureFY2022 update

- Hiroshi Nishiura (Professor, Graduate School of Medicine and Faculty of Medicine Kyoto University)
- PRESTO
- Innovative model of biological processes and its development “Statistical modelling of infectious diseases and their non-pharmaceutical interventions using existing informative data” Researcher (2009-2013)
- RISTEX
- Realizing Policymaking Process of Infectious Disease Control using Mathematical Modeling Techniques, Principal Investigator (2014-2017)
- CREST
- Advanced Application Technologies to Boost Big Data Utilization for Multiple-Field Scientific Discovery and Social Problem Solving “Detecting premonitory signs and real-time forecasting of pandemic using big biological data” Research Director (2014-2021)
From “experience and intuition” to objective evaluation
Epidemics of infectious diseases such as dengue fever and HIV have had profound impact on human health and society. Controlling these diseases is a common challenge in all societies, especially in the modernized world, where infectious disease control plans are demanded at policy level, in addition to merely the development and improvement of effective medical technologies. “Infectious disease modelling” studies of Professor Hiroshi Nishiura, the Principal Investigator of RISTEX, are anticipated as an effective tool for such policy planning.
Infectious disease modelling uses numerical mathematical formulas and describes the process of infectious disease transmission, incubation period from the time of infection to illness onset, and how the disease progresses in the infected host. In our modelled society, epidemic of infectious diseases can be reproduced in the computer, countermeasures are hypothetically considered as scenarios, and efficacy of the implemented policy is thereby objectively evaluated. The quantitative validity and accuracy of mathematical modelling approaches have improved drastically in the last 15 years, and expert groups of mathematical models also play a role as a brain of governmental organizations for policy making in the country. Infectious disease modelling is now widely used in the process of creating health care policies, especially in Europe.
On the other hand, in Japan, every time an epidemic of infectious diseases is recognized as a social problem, experts of infectious diseases and epidemiology have been invited to a meeting to analyze the observed data, improve our situation awareness and even decide public health responses to the epidemic; in other words, measures such as vaccination were taken based on “experience and intuition”. If clear evidence could be brought into policy-making based on the present mathematical modelling, infectious diseases should be controlled more effectively.
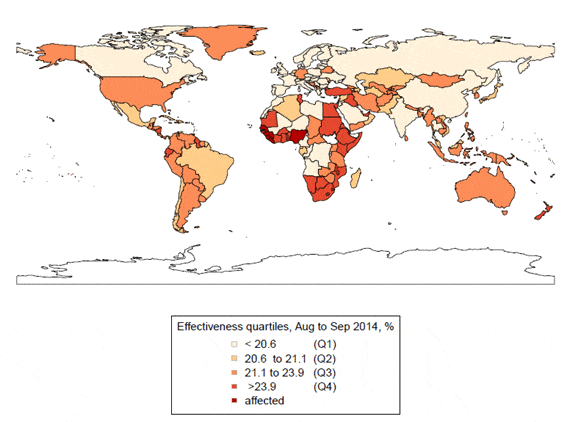
Estimated reduction effect of epidemic risk of Ebola hemorrhagic fever due to travel restrictions calculated by using a mathematical model
(revised from Otsuki S & Nishiura H, PLoS One 2016)
If additional adult men possessed immunity, rubella outbreak would not have occurred
What can be achieved by using mathematical models? A typical application is to estimate vaccination target and amount. We can calculate the percentage of population that needs to be vaccinated and acquire immunity in order to prevent a major epidemic.
In Japan, there was a rubella outbreak from 2012 to 2013. When the data were analyzed, it became clear that adult men played a central role in the epidemic. Routine vaccination for rubella was only given to female junior high school students until 1994; thus, by 2010, there were many adult men without immunity. Professor Nishiura took into account this point into the rubella transmission model, calculating theoretical conditions required to prevent future rubella outbreaks. The result was that specifically, if men in their 30s to 50s were vaccinated, it could prevent major epidemics in the future. Results of professor Nishiura and his colleagues became an important theoretical basis in planning for routine (supplementary) vaccination for these age groups.
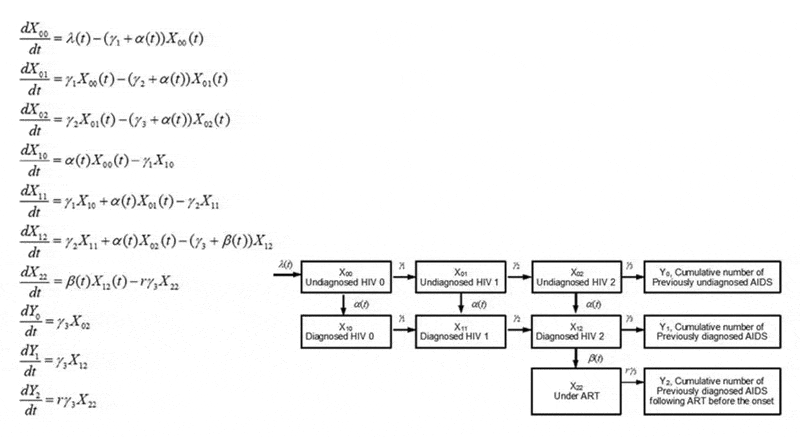
A mathematical model of infectious diseases
A system to estimate AIDS patients was proposed
When the director of the National Institute of Infectious Diseases was informed that men in their 30s to 50s should be given priority in vaccination, and its required budget, a new project started, and there have been discussions on the goals of vaccination programs. As for vaccinations, we have been interacting with the health care policy makers. Numerical experiments have been performed for various scenarios, which were prepared for questions such as what happens if the age group was narrowed down to 30s to 40s, and what happens if men and women were vaccinated with an equal frequency. Through this research and development, we were able to contribute to making revisions to prevention policies of Ministry of Health, Labour and Welfare against infectious diseases, and to estimation of the cumulative incidence throughout the course of rubella outbreaks.
In addition, we conduct modelling studies on HIV/AIDS. It takes several to ten years to the onset of AIDS following an HIV infection, but unless blood is voluntarily tested at a medical facility, HIV infection cannot be recognized and detected. There had not been any official estimate of the number of patients unaware of HIV infection in Japan. Thus, Professor Nishiura used a mathematical model, and proposed a framework that estimates undiagnosed HIV infected patients based on the number of reported HIV infected patients and AIDS patients.
As such, policy-making that could not be observed in the past could be logically discussed while maintaining a certain level of scientific validity. This is one of the core contributions of mathematical modelling to policy settings.
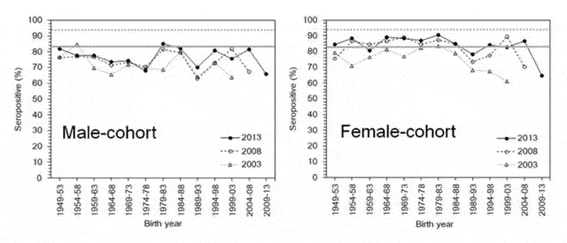
Suggestions for vaccinations
Source: Revised from Kinoshita & Nishimura (2016).
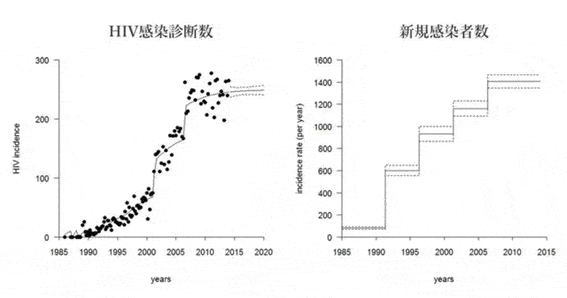
Suggestions for HIV/AIDS countermeasures
Improving literacy is an important issue
Achievements of Professor Nishiura and his colleagues attracted an attention from the public as rubella outbreak developed to a social problem, and were widely publicized by major online media and news websites. It became possible for healthcare policy personnel and researchers have discussions after presenting multiple epidemic scenarios and their budgets. Having insights from mathematical modelling is truly a revolution for administration side as well.
In the future, an important issue is to increase the literacy for infectious disease modelling for proper communications. Infectious disease modelling is a field of research in which the next development comes about by having policy makers refers to research results; thus, the ideal situation is that the relationship between the government and researchers is equal, and progresses by receiving the needs of the other side continuously.
Mathematical modelling is also useful for various fields other than vaccination. For example, the model could be used for predicting a collapse in the demand and supply balance in the industry due to changes in the population structure in Japan, which faces unprecedented population aging, and propose necessary countermeasures. It could also help predict disease risk and prevent epidemic such as tuberculosis and HIV accompanying a large-scale increase in the number of foreign laborers. If certain evidences are brought in based on a mathematical model, and policies are formed by it, not only can the effects of policy increase, but also the cost reduction can be expected.
