ERATO(Exploratory Research for Advanced Technology)
Hirayama Nuclear Spin Electronics Project
Supported by JST(Japan Science and Technology Agency)

1. Manipulation of nuclear spins in GaAs quantum systems and highly-sensitive NMR

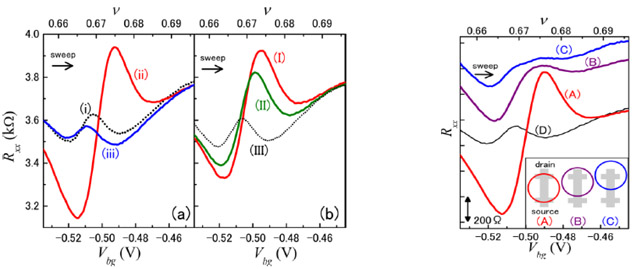
Optically pumped nuclear polarization and its resistive detection Nuclear spins in a single quantum well are polarized by optical pumping and its polarization is detected by a shift of the resistance peak of the SPT (spin-phase-transition) at Landau level filling factor ν = 2/3. The sample used in this experiment is a 30-μm wide and 100-μm long Hall bar, which was processed from a wafer containing an 18-nm GaAs/Al0.33Ga0.67As quantum well (QW). The electron density is controlled by the back gate voltage, Vbg. A mode-locked Ti:sapphire laser (wavelength: 809.2 nm, pulse width: ~2 ps, and pulse repetition: 76 MHz) is used for optical pumping. The beam diameter on the sample is about 200 μm. The propagation direction of the laser is parallel to static magnetic-field, B, which is perpendicular to the QW. The measurements were performed at B = 7.1 T and the temperature of 320 mK. First, the laser beam is injected into the center of the Hall bar. The intensity profile in the Hall bar is almost homogeneous in this case. Figure 1(a) shows the laser polarization dependence of Rxx as a function of Vbg. The SPT peak is shifted to a positive and negative direction in (ii) σ+ and (iii) σ-　illumination, respectively. Application of resonant-frequency rf magnetic-field induces the peak shift, confirming optically pumped nuclear polarization is really detected by the resistance measurement (see Fig. 1(b)). Second, we study the spatial dependence of optical nuclear polarization. Figure 2 shows the SPT peak by changing the laser injection position from the center of the Hall bar to the drain (see inset). The SPT peak becomes broader and smaller from (A) to (C). As the illumination area is moved to the drain, the gradient of the laser intensity in the Hall bar increases. Since the magnitude of nuclear polarization depends on the laser intensity, the BN distribution broadens as the intensity gradient increases. Controlling polarization, power, time, and beam profile of laser illumination will enable us to manipulate the nuclear spin orientation and to create various spatially modulated nuclear spin profiles in the future.

Fig. 1. (a) Laser polarization dependence of SPT peak: (i) no optical pumping, (ii) σ+, and (iii) σ- illumination. (b) RF modulation dependence　of SPT peak: (I) RF off-resonance with 75As, (II) RF on-resonance　with 75As, and (III) no optical pumping.		Fig. 2. (A)-(C): SPT peak with σ+ illumination for three　irradiation positions as shown in inset.
Pubication: K. Akiba, S. Kanasugi, K. Nagase, and Y. Hirayama, Appl. Phys. Lett. 99, 112106 (2011).

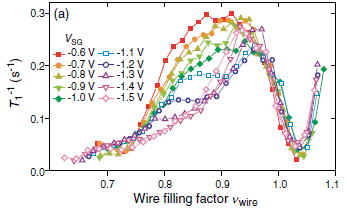
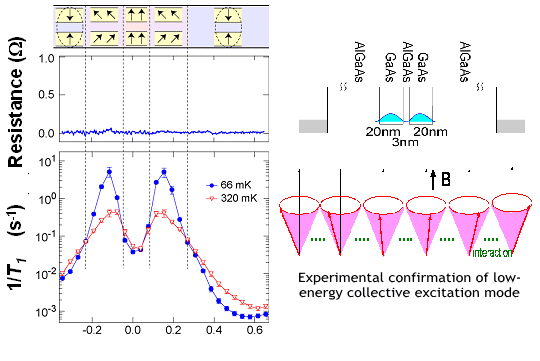
Low-frequency spin fluctuations in Skyrmions confined by wires Low-frequency spin fluctuations associated with the XY spin component in Skyrmions have been manifested as fast nuclear spin relaxation in GaAs two-dimensional systems. In this study, we have extended such nuclear relaxation measurement to quasi-one-dimensional wires. We have developed a technique to measure the local nuclear spin relaxation rate T1-1 in the wire with a typical width and length of 500 nm and 3 μm, respectively. The technique is based on the selective polarization of nuclear spins inside the wire and resistive detection of the polarization. Figure 1 shows T1-1 as a function of νwire for several values of VSG. The transverse distribution of the filling factor in the wire is obtained by numerically solving the Poisson equation under zero magnetic field, and νwire is defined as the filling factor at the center of the wire. The appearance of a minimum at νwire = 1.03 and a peak aroundνwire = 0.9 is similar to the behavior of T1-1 in the bulk 2DESs, where the minimum appears atν = 1 and the T1-1 enhancement on both sides ofν = 1 is explained by spin fluctuations associated with Skyrmions. The similarity indicates that Skyrmions exist in the wire. The small deviation of the minimum position fromνwire = 1 is ascribed to calculation errors ofνwire. In the range of 0.1< νsky in wire <0.3, where Skyrmion density (νsky in wire) is defined as νsky in wire=∣1.03-νwire∣,T1-1 shows the strong VSG dependence. As VSG is decreased, T1-1 decreases and then saturates. The wire width is larger than the individual Skyrmion size so that this feature suggests modification of the multi-Skyrmion state and related suppression of the low-frequency spin fluctuations by the wire confinement. We speculate that the Skyrmion crystal is melted into the Skyrmion liquid as the wire becomes narrower. As shown here, highly-sensitive nuclear-spin-related measurements provide us powerful tool to study electron spin physics in a quantum confined system.

	Fig. 1 T1-1 as a function of the numerically calculated νwire for several values of VSG
Pubication: Takashi Kobayashi, Norio Kumada, Takeshi Ota, Satoshi Sasaki, and Yoshiro Hirayama, Phys. Rev. Lett. 107, 126807 (2011).

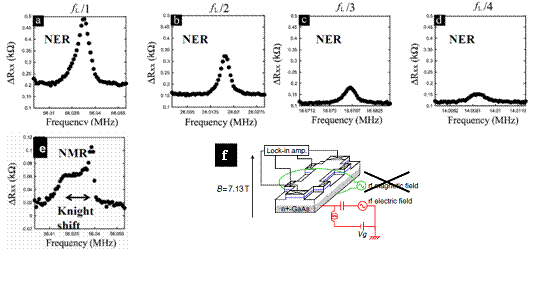
NER (Nuclear Electric Resonance) based on electron-spin/nuclear-spin interactions An alternative nuclear spin resonance using a radio frequency (rf) electric field instead of a magnetic field has been demonstrated by using the electrical control of the electron-spin domain structures. Spin-polarized and -unpolarized electron states energetically degenerate at ν = 2/3 spin phase transition point, resulting in a formation of domain structures. One can use this domain structures to realize nuclear resonance driven by fully electrical method, i.e., NER. In this NER, oscillating electric field induces a domain wall (DW) oscillation. Because the DW has a finite in-plane hyperfine component, BxHF, nuclear magnetic resonance is induced when DW goes back and forth on the polarized nuclear spin site and nuclear spins effectively feel oscillating in-plane magnetic field with resonant frequency. Nuclear spins are manipulated only by electric field so that high spatial sensitivity can be expected. In the NER experiment, a sinusoidal rf voltage is applied to the backgate through a bias-tee (see (f)) after dynamic nuclear spin polarization. The NER spectra were recorded by plotting the resistance variation, R, which is extracted by subtracting value of resistance after rf application from that of before, as a function of rf frequency as shown (a) – (d). The resistively-detected NMR mediated by oscillating magnetic field is also shown in (e) as a reference. The NER signal appears not only around fL but also around fL /2, fL /3 and fL /4 differently from NMR. The BxHF produced by a domain wall oscillation has not sinusoidal but pulse-like shape, which includes a certain amount of harmonic components. Therefore, existence of harmonic component confirms us that signals observed in (a)-(d) are actually arising from electrically-induced domain motion. It should be stressed that NER and NMR signals shown in (a) and (e) have slightly different. The NMR spectrum has two peaks and high (low) frequency peaks are arising from nuclear spins interacting with unpolarized (polarized) ν = 2/3 domains, respectively. The nuclear spins located in the spin polarized domain feel a finite BzHF; however, those in the spin unpolarized domain feel zero BzHF. The separation between two peaks corresponds to the Knight shift. Whereas, domain walls oscillate in the NER and nuclear spins feel average BzHF some value between finite and zero BzHF. The NER signal observed in (a) actually lies between two NMR peaks, suggesting averaged Knight shift .

Pubications: N. Kumada, T. Kamada, S. Miyashita, Y. Hirayama, and T. Fujisawa, Phys. Rev. Lett. 101 137602 (2008). S. Watanabe, G. Igarashi, K. Hashimoto, N. Kumada, and Y. Hirayama, Physica E42 999 (2010)

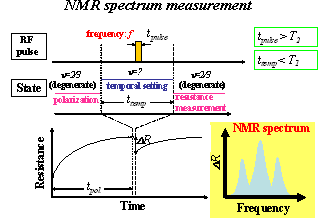
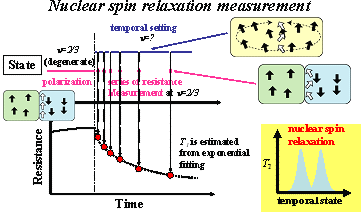
Resistively-detected nuclear-spin-based measurements

NMR (Nuclear Magnetic Resonance) is widely used to chemical, medical and physical studies. In spite of its excellent performance, however, NMR application to semiconductor systems, which play essential roles in recent electronics and cutting edge solid-state physics, is limited due to the low sensitivity of conventional NMR. Conventional NMR based on induction-detection requires multiple layers (more than 40, for example) of quantum wells to achieve a sufficiently high signal-to-noise ratio and is not suitable for the analysis of semiconductor layer and nano structures where characteristics are controlled by the gate biases. Recently, we have demonstrated dynamic nuclear spin polarization induced by a current flow and, furthermore, resistance detection of nuclear spin polarization. The linear relation is satisfied between the resistance value and the magnetization, Mz, of nuclear spins. Resistance can be measured for a single layer and even for a nanostructure, so we can extend the powerful feature of NMR to studies of semiconductor systems. The following figures illustrate examples how we can get NMR spectrum and nuclear spin relaxation time (T1) by using a novel resistance detection technique. It should be stressed that we need special states (degenerate states) at ν=2/3 for dynamic nuclear polarization and its resistance detection, but we can apply these measurements for any states which we want to estimate.

Study of electron spin features by using nuclear-spin-based measurements

Nuclear spins, especially their relaxation, can be used as a sensitive detector of electron spin systems. This is because the nuclear spin relaxation rate (1/T1) is strongly enhanced when the spectral density of transverse electron-spin fluctuation has the component corresponding to the NMR frequency of nuclear spins. This unique feature can be extended to unveil collective electron spin characteristics, which are difficult to detect in conventional transport and optical measurements.
By using nuclear-spin-based measurements, we have recently succeeded to show clear evidence of the canted spin states in ν=2 bilayer system and related low-frequency spin fluctuation arising from the breaking of the planar symmetry (see the following figures). The spin degree of freedom in ν=1 bilayer system and enhancement of electron spin fluctuation under strongly asymmetric confinement were also successfully detected. These results confirm us that nuclear-spin-based measurements will play an important role to study the electron spin features in semiconductor hetero and nanostructures.

Publications:
N. Kumada, K. Muraki, K. Hashimoto, and Y. Hirayama, Phys. Rev. Lett. 94, 096802 (2005).
K. Hashimoto, K. Muraki, N. Kumada, T. Saku, and Y. Hirayama, Phys. Rev. Lett. 94, 146601 (2005).
N. Kumada, K. Muraki, and Y. Hirayama, Science 313, 329 (2006).
N. Kumada, K. Muraki, and Y. Hirayama, Phys. Rev. Lett. 99, 076805 (2007).
＊

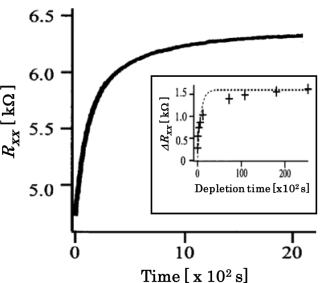
Electron spin/ nuclear spin interactions at ν=2/3 and dynamic nuclear polarization

The interaction between electron and nuclear spins occurs in the fractional quantum Hall regime in case that two different spin states have degeneracy. The interaction has been evidenced by slow and gradual resistance enhancement observed at the certain condition. The involvement of the nuclear spin polarization in this resistance enhancement has been confirmed by nuclear magnetic resonance (NMR) experiments under a radio frequency irradiation and a long-term memory effect after a complete depletion of the 2DEG.
We also found that the spin phase transition (SPT) from spin-polarized to spin unpolarized ν=2/3 gives us a very sensitive measure of the background nuclear polarization. The less than 1% nuclear polarization can be detected as a shift of the SPT peak position. In the case of dynamic nuclear polarization by the current flow at ν=2/3 SPT, nuclear polarization occurs spatially inhomogeneous manner, resulting in the SPT peak with an enhanced amplitude and a large half-width. By using the characteristics of the SPT, we also confirm that the spin-unpolarized (spin-polarized) domain mainly mediates the up-directed (down-directed) nuclear spin polarization.
Left-figure: A grey-scale plot of Rxx at T = 80 mK as a function of magnetic field and electron filling factor was measured by scanning the electron density at the normal speed with a small current. This figure shows intrinsic characteristics of electronic states. The transition from spin-polarized to spin unpolarized ν=2/3 is clear and we can see the degenerate states between them. When we measured Rxx using a slow scanning rate with a larger current, Rxx enhancements appear at the points of the white circles which size corresponds to the value of the Rxx enhancement. The Rxx enhancements clearly occur along the transition point between spin-polarized and unpolarized ν=2/3 states by the dynamic nuclear spin polarization.
Right-figure: The gradual polarization of nuclear spins results in the slow Rxx increase as a function of time when we set the sample to the ν=2/3 degenerate point. The gradual Rxx increase also means that we can measure the degree of nuclear spin polarization by using the Rxx value. To confirm this point further, we completely deplete 2DEG after nuclear spin polarization, in other words Rxx saturation, for certain time duration and measure how Rxx enhancement relax during this duration. The resistance relaxation,ΔRxx, is approximately fit the exponential decay with a time constant of about 1000s. This time constant agrees well with T1 time of nuclear spins estimated from conventional NMR experiments. This result suggests unique and important feature of the interaction at the ν =2/3 degenerate situation; approximately linear relation between Rxx value and total longitudinal magnetization,Mz, coming from nuclear spin polarization.

Publications:
K. Hashimoto, K. Muraki, T. Saku and Y. Hirayama, Phys. Rev. Lett. 88 176601 (2002)
K. Hashimoto, T. Saku and Y. Hirayama, Phys. Rev. B 69 153306 (2004)
M. H. Fauzi, S. Watanabe, and Y. Hirayama, J. Korean Phys. Soc. 60,1676 (2012).
M. H. Fauzi, S. Watanabe, and Y. Hirayama. App. Phys. Lett. 101, 162105 (2012).

Study on ν = 5/2 spin state

The FQH effects appear for many magic fillings with ν = p/q (p,q: integer). The composite-fermion (CF) scenario, in which an electron is transformed into a fictitious particle by combining it with an even number of flux quanta, can explain FQH effects for odd values of q. The most well-known FQH effects can be explained with this scenario like the ν = 2/3 extensively discussed in this project. However, there are even denominator FQH states, which cannot be described within the simple CF scenario. The most notable example is the ν = 5/2 FQH state, which was observed for extremely high-mobility GaAs quantum systems at extremely low temperatures. This ν = 5/2 FQH effect has recently attracted a great deal of attention, as its ground state may have quasi-particle excitations obeying non-Abelian statistics, which are suitable properties for topologically-protected error-tolerant quantum computers. The RD-NMR measurements based on ν= 2/3 SPT have recently been successfully applied to the ν = 5/2 state. From its Knight shift, the ν = 5/2 state was confirmed to be fully spin polarized. These RD-NMR measurements provided strong support for the ν = 5/2 state being non-Abelian. The experimental results also indicate an intrinsically different nature of interaction in the ground and first excited Landau levels. The spin polarization in the ground (n = 0) LL between ν = 2 and 1/3 estimated from the NMR Knight shift exhibits a complicated oscillatory pattern reflecting the various CF ground states. In contrast, spin polarization in the first excited (n = 1) LL increases linearly for ν ≥ 2.2 across ν = 5/2, indicating that the system is fully polarized over a wide range.

Publications:
L. Tiemann, G. Gamez, N. Kumada and K. Muraki, Science 335, 828 (2012).

2. Coherent control and multiple-pulse sequence

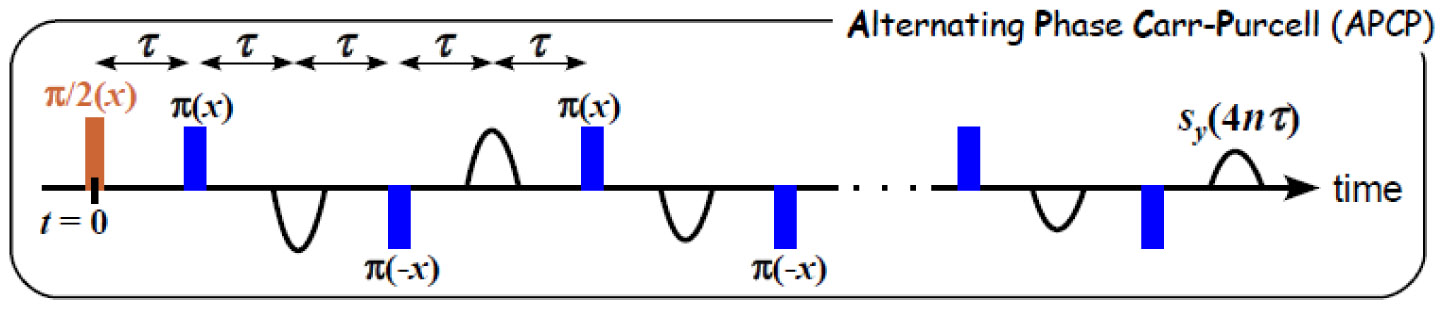
Measurement of the noise spectrum using a multiple-pulse sequence A method is proposed for obtaining the spectrum for noise that causes the phase decoherence of a spin (qubit) system directly from experimentally available data. The method is based on a simple relationship between the spectrum and the coherence time of the spin (qubit) in the presence of a pulse sequence. Here, we assume a simple sequence of equidistant pulses such as an APCP (shown in Fig. 1) or CPMG sequence. In the long time limit (large pulse number limit) keeping the interpulse time (2τ) fixed, we find that the coherence exhibits an exponential decay. This time dependence enables us to define uniquely the coherence time T2L for a multiple-pulse sequence. We call the obtained T2L as ‘‘generalized’’ coherence time, because this T2L indicates T2 time for a certain frequency in contrast to the Hahn echo T₂ reflecting a static T₂ time. More interestingly, this generalized T₂^L has a simple relation with a noise spectrum S(ω) as

Since the factor 1/(2l+1)2 is smaller for larger l, we can approximate the above equation into

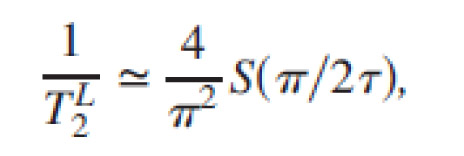if S(ω) rapidly decreases as ω increases. These relationships are qualitatively explained as follows. In many systems, coherence time is dominated by the lowest-frequency component of the noise spectrum (fluctuation-dissipation relation). The pulse sequence with time interval ~τcancels out the noise at frequencies lower than 1/τ (dynamical decoupling). Therefore, the noise spectrum around the frequency 1/τ dominantly contributes to the coherence time in the presence of the pulse sequence. The relationship is found to hold for every system of a spin (qubit) interacting with the classical-noise, bosonic, and spin baths. 　The proposed noise spectrum measurement provides us very useful method to evaluate the noise spectrum of spin, nuclear spin, and many types of qubits.

	Fig. 1 Example of the pulse sequence
Pubication: Tatsuro Yuge, Susumu Sasaki, and Yoshiro Hirayama, Phys. Rev. Lett. 107, 170504 (2011).

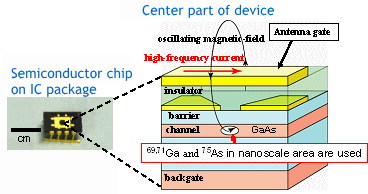
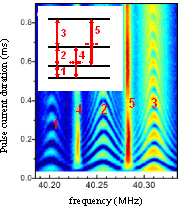
Coherent control of nuclear spins in point contact device The electron spin /nuclear spin interactions have been extended into a nanoscale structure and coherent oscillation of nuclear spins are directly detected as a resistance oscillation. Top figure: Schematic diagram of the device used in this research. This equipment creates interaction between electron and nuclear spins in a nanoscale area of 200 nm x 200 nm x 10 nm (point contact). When an electric current is applied to this tiny area, polarization of the nuclear spin is observed only in this area. When an alternating current is applied to an antenna, the current produces an alternating magnetic field. If this field resonates with the nuclear spin Lamor frequency, the quantum-mechanic control of the nuclear spins is achieved. Although standard NMR requires a specimen of a size approaching the level of cm, this device is a fine semiconductor chip, the core part of which is in the order of nanometers. The compactly integrated structure has opened the way for nuclear spin control with unprecedented precision. Bottom figure: The quantum-mechanic superposition can be well controlled between four separated states peculiar to the nuclei of gallium (Ga) and arsenic (As), which constitute the nano-device. The successful control of nuclear spin with a nano-device, which is notably all-electrical control, was a significant step forward towards nuclear spin quantum computers. The technology developed is also attractive as a nanoscale NMR technology with an extremely small volume of material.


Publications: G. Yusa, K. Muraki, K. Takashina, K. Hashimoto and Y. Hirayama, Nature, 434, 1001 (2005). Y. Hirayama, A. Miranowicz, T. Ota, G. Yusa, K. Muraki, S. K. Ozdemir, and N. Imoto, J. Phys.: Condens. Matter 18, S885(2006). T. Ota, G. Yusa, N. Kumada, S. Miyashita, and Y. Hirayama, Appl. Phys. Lett. 90, 102118 (2007). ＊

3. Parallel magnetic-field experiments and resistively-detected NMR in InSb quantum systems

Nonlinear spin polarization in InSb 2DEG The spin polarization (P) of high-density InSb two-dimensional electron systems (2DESs) has been measured using both parallel and tilted magnetic fields for InSb quantum wells. Resistance spikes arising Landau-level crossing in the tilted field and resistance spike (or shoulder) in the parallel field were used to determine spin-polarization (P) and critical field (Bc) where P=1. P is found to exhibit a superlinear increase with the total field B. This P-B nonlinearity results in a difference in spin susceptibility between its real value χ_s and χ_gm. Temperature-dependent amplitude analysis of low-field SdH oscillations (the so-called Dingle plot) suggests a P-independent m. Accordingly, the P-enhanced gm is attributed to the increase of g. Our results indicate successful fitting to the simple equation.

Such linear P-dependent g* might be explained by the exchange coupling of electrons. A significant change of g* (g*= 49) from 39 at P = 0 to 88 at P = 1 was obtained in our InSb 2DES. The present result has led us to reconsider the interpretation of previous work on a low-density GaAs 2DES, where a similar P-B nonlinearity is believed to be due to the electron-correlation contribution. For general scientific summary (background, main results and wider implication) of this research, please also refer homepage of New Journal of Physics　(http://iopscience.iop.org/1367-2630/13/8/083010/)

	Fig. 1 (a) Spin polarization P versus the normalized field Bp/Bc. (b) χ_s and χ_gm versus P.
Publication: K. F. Yang, H. W. Liu, K. Nagase, T. D. Mishima, M. B. Santos, K. Nagase, and Y. Hirayama, New Journal of Physics 13, 083010 (2011)

Resistively-detected NMR of InSb at high temperatures Highly-sensitive resistively-detected NMR (RD-NMR) has been demonstrated for typical narrow-gap system, a single InSb quantum well. This RD-NMR of InSb 2DEG was recently extended to high temperature regime. The RD-NMR and T1 measurements were performed by using Landau-level crossing at =2 similar to the previous report (H. W. Liu et al., Phys. Rev. B82, 241304(RC) (2010)). However, in this experiment, we use a DC current in place of an AC current, because the RD-NMR signal becomes stronger in DC than that in AC for this sample. The RD-NMR signal obtained for DC current shows a peak-dip line shape in Rxx in contrast to the RD-NMR spectrum with only a dip or a peak under the AC current. Such a dispersive RDNMR signal has also been demonstrated in GaAs 2DEGs, but the underlying mechanism remains obscure. The RD-NMR signal of 115In can be detected up to 4 K as shown in Fig. 1, although the signal amplitude decreases with temperature. We suggest that this upper limit temperature corresponds to the Curie temperature of the Ising quantum Hall ferromagtneto at =2 Landau-level crossing. One can expect a modification of hopping transport when the domain wall collapses at the Curie temperature. Actually, as shown in Fig. 2, Rxx value of the resistance spike at the =2 Landau-level crossing deviates from the fitting based on the hopping transport at around 4 K. We also found almost constant T1 time independent of temperature in this experiment. The InSb 2DEG with large Zeeman, cyclotron, and exchange energies is a suitable candidate for implementation of the nuclear-spin based information processing at high temperatures.

Fig. 1. RD-NMR signal of ¹¹⁵In at T = 1K and 4 K. ⊿Rxx is the resistance change induced by the nuclear depolarization, when frequency of the oscillating magnetic field is swept through the Larmor resonance of ¹¹⁵In.	Fig. 2. (a) Temperature dependence of longitudinal resistance Rxx vs the total magnetic field B at a tilt angle of 64.5° . The resistance spike at the filling factor of ν=2 (B~12.3 T) is the signature of QHF. Inset: setup of the tilted-magnetic-field experiment. (b) Spike amplitude as a function of I_dc (square) at T=100 mK and temperature (circle) at I_dc=10 nA. The solid line is a fit to the temperature dependence using the variable range hopping model.
Pubication: K. F. Yang, H. W. Liu, K. Nagase, T. D. Mishima, M. B. Santos, and Y. Hirayama, Appl. Phys. Lett. 98, 142109 (2011)

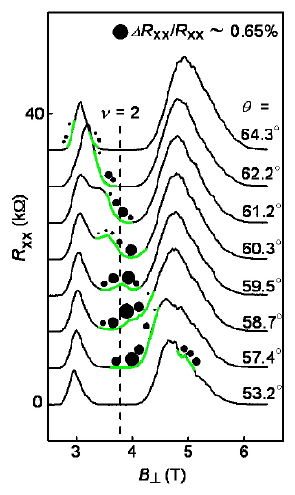
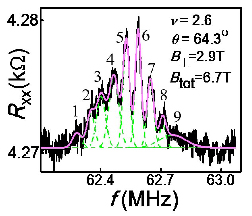
Highly-sensitive resistively-detected NMR of InSb two-dimensional systems It is exciting to extend highly-sensitive resistively-detected (RD) NMR to narrow-gap semiconductors including indium (In). Narrow-gap semiconductors attract much attention from the viewpoints of “Beyond Si” devices and spintronics applications. Successful RD-NMR will provide a new pathway for unveiling the electron spin characteristics of narrow-gap 2D through NMR spectrum and T1 time measurements. Moreover, indium-115 is a unique nuclear spin with I = 9/2, where nuclear spin states separate into ten. Such ten-level-system gives us exciting opportunity to coherently control multiple-quantum-levels toward nuclear-spin-qubit. In spite of such interests, highly-sensitive RD-NMR was limited in GaAs quantum systems over the past 20 years. Recently, we have succeeded to demonstrate RD-NMR for typical narrow-gap system, a single InSb quantum well. Differently from GaAs systems, a degeneration of the different spin states is realized by tilting the sample in a magnetic field. Extremely large g-factor of InSb results in a crossing of down spin of ground Landau-level (LL) and up spin of the first LL at = 2 as evidenced by a resistance spike shown by green lines in Fig. 1. We can expect a formation of the simplest pseudospin (involving spin and Landau-level) quantum Hall ferromagnet with a domain structure at this crossing. By flowing current at this crossing, dynamic nuclear polarization and RD-NMR have been demonstrated for both In and Sb nuclei. As already mentioned, 115In has I = 9/2 and transitions between neighboring states form nine peaks with equal interval in the NMR spectrum under quadrupolar splitting. Such separation is clearly observed in the experiments as shown in Fig. 2. The solid circles in Fig. 1 indicate positions where RD-NMR can be detected and the size of circle corresponds to the amplitude of RD-NMR signal. The obtained results confirm nuclear spin polarization and RD-NMR only around resistance spike arising LL crossings, suggesting essential role of quantum Hall ferromagnet state and domain formation.

	Fig.1 Resistance spike observed at ν=2 for tilted magnetic field experiment. Solid-state circles indicate positions where RD-NMR can be detected.	Fig.2 RD-NMR signal of 115In measured at T=100mK. The data was obtained from the spike inside the LL peak at θ=64.5°in Fig.1. The solid line is a fit with nine Gaussian curves(dashed line).
Pubication: H. W. Liu, K. F. Yang, T. D. Mishima, M. B. Santos, and Y. Hirayama, Phys. Rev. B 82, 241304(RC) (2010) [editor’s suggestion]

Successful gate control of InSb quantum wells with ALD gate dielectrics

The successful gate control of InSb two-dimensional systems is essential to extend our RD-NMR and spin-susceptibility studies to the wider-range pump-and-probe experiments. To achieve this goal, high-quality Al2O3 dielectrics were grown by atomic layer deposition (ALD) on InSb quantum wells. Magnetotransport measurements were carried out to clarify the characteristics of a gated InSb quantum wells. When we deposited Al2O3 dielectrics on InSb top layer, the magnetoresistance data demonstrate a parallel conduction channel at zero gate voltage (Vg). A good interface between Al2O3 and the top InSb layer ensures that the parallel channel is depleted at negative Vg and the density of two-dimensional electrons in the QW is tuned by Vg with a large ratio of 6.5 × 10¹⁴ m^-2V^-1 but saturates at more negative Vg. These findings are closely related to layer structures of the quantum wells. The better controllability without parallel conduction appears when we deposited Al2O3 dielectrics directly on InAlSb barrier layer.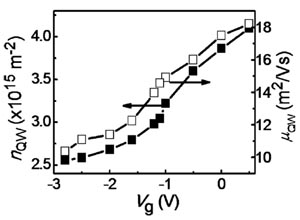

Fig. 1 Electron density and mobility of the 2DEG confined in the InSb QW as a function of Vg. Measurements were performed at 2K.

Publications:
M. M. Uddin, H. W. Liu, K. F. Yang, K. Nagase, T. D. Mishima, M. B. Santos, and Y. Hirayama, Appl. Phys. Lett. 101, 233503 (2012)

4. Nanoscale spatial observation of 2D systems

Scanning probe microscopy of the quantum Hall States When water transforms into steam, or magnetized iron changes to demagnetized iron, phase transition takes place. Such classical phase transitions often share many fundamental characteristics near the critical point. Quantum phase transitions also show universal critical behaviors which is affected by not only temperature but also quantum mechanics. The real-space observation of rather complex phenomena due to quantum mechanics is the key access to a descriptive understanding. Two-dimensional electron systems such as the integer quantum Hall system are considered as paradigms for the study of quan¬tum phase transitions. Although macroscopic aspects of the percolative behavior of the systems have been verified, the perhaps most fundamental aspect, i.e. how electron wave functions change across the transition, has not been tackled experimentally. We demonstrate the first real space observation of a quantum Hall transition by performing scanning tunneling spectroscopy on "surface" two dimensional electron system at low temperature (0.3 K) and high magnetic field (up to 12 T). In accordance with theoretical predictions, we find localized electronic states at ener¬gies of the Landau level tail and extended drift states at energies correspond¬ing to the Landau level center. The observed microscopic behavior reveals that quantum tunneling plays a key role in this quantum phase transition. We also clarify a robust nodal structure of Landau Level wave functions by using fourier transform scanning tunneling spectroscopy. Our findings demonstrate that Landau quantization implies disorder independent universal features on the microscopic scale. This complements the well-known universal quantum Hall plateaus.

		Figure Experimentally determined Landau fan diagram recorded by dI/dV(Vs )-spectroscopy at the same position and at changing B. Spin-down LLs of the 1st (2nd) subband are marked by green (red) dashed lines and spin levels by arrows.

		Evolution of the quantum Hall transition The movie shows the continuous change of the LDOS with energy measured for the lowest Landau level at B = 12 T. Spatial isolated closed-loop patterns (localized states) observed at energies of the Landau level tail becomes partly connected at saddle points of the potential and evolve to dense network (extended states) at energies corresponding to the Landau level center.
Pubication: K. Hashimoto, C. Sohmann, J. Wiebe, T. Inaoka, F. Meier, Y. Hirayama, R. A. Romer, R. Wiesendanger, M. Morgenstem, Phys. Rev. Lett.101 256802 (2008) K. Hashimoto,T. Champel,S. Florens, C. Sohrmann, J. Wiebe, Y. Hirayama, R. A. Roemer, R. Wiesendanger, and M. Morgenstern, Phys. Rev. Lett. 109, 116805 (2012)

＊This study was completed before starting ERATO-NSEP project.