事業成果
コンピューターの処理回数を大幅に圧縮
超高速アルゴリズムを開発2017年度更新

- 湊 真一(北海道大学 大学院情報科学研究科 教授)
- ERATO
- 「湊離散構造処理系プロジェクト」 研究総括 (H21-26)
膨大な組み合わせを超高速に列挙する
不可思議という単位がある。万、億、兆、京などと続く数の単位で10の64乗のことだ。実は、電車の乗り換えや電気の配電網など、さまざまな組み合わせの中から最適なものを選ぼうとすると、その選択肢は10の64乗という膨大な数になることも珍しくない。これを短時間・低コストで1つ1つ列挙して、最適なものを選ぶにはどうしたら良いか。そのカギを握る技術が、処理の計算手順・戦略を記述して最適な答えを効率的に導き出すアルゴリズムだ。
現在コンピューターは、産業プロセスの最適化や解析、マーケティング、バイオインフォマティクス(生命情報科学)など、さまざまな情報処理に活用されている。近年、爆発的に増大しているビッグデータを処理するために、ハードウェアの高速化とともに、アルゴリズム技術の重要性が高まっており、その高速化が求められている。そこでERATO研究総括の湊真一教授は、離散構造(記号によって表現される概念)を極めて高速に処理するための離散構造処理系の研究に取り組んだ。
コンピューターの処理回数を圧縮する
この研究の基盤となったのが、湊教授が1993年に考案し、世界的にも注目されているZDD(ゼロサプレス型BDD:Zero-suppressed BDD)である(図1)。基本的な離散構造の1つに論理関数があり、一般に論理関数の値をすべての変数について場合分けした結果は二分決定木(Binary Decision Tree)として表現できる。コンピューターの処理に置き換えると、分岐の数は処理の回数を意味する。処理回数を減らすための工夫として、BDD(Binary Decision Diagram)というデータ構造を用いたアルゴリズムが1986年に米国で考案された。湊教授が考案したZDDは、このBDDを集合データの処理に進化させたもので、特に「疎な組み合わせの集合」、例えば1万アイテムの商品から10アイテムを選び出すといった、巨大な母集団から非常に少数を抽出するようなケースで、処理回数を大きく圧縮できる。ケースにもよるが、ZDDを使えばBDDよりもさらに数十~数百倍の圧縮が可能になる場合があるという。
図1
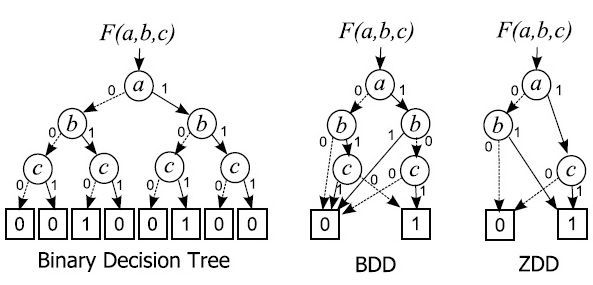
右のZDDが、湊教授が考案したゼロサプレス型BDD
スマートグリッドの最適化に成功
湊教授らは、BDDとZDDの技法をさらに発展させ、多様な離散構造を統合的に演算処理する技法を体系化した。システム検証や最適化、データマイニング、知識発見などを含む分野横断的かつ大規模な実問題をより高速に処理することを目指したのだ。その成果の1つにフロンティア法と呼ばれる手法の開発とその応用が挙げられる。フロンティア法は、一般的なグラフ構造の形で制約条件が与えられたときに、条件を満たす組み合わせをすべて列挙するZDDを超高速に構築する手法で、さまざまな社会インフラの解析等での応用が進んでいる。例えばスマートグリッドと呼ばれる電力網の解析が挙げられる。変電所設備72か所、スイッチ数468個からなる典型的な電力網において、天文学的に膨大なスイッチ構成(ON/OFF)の組合せを世界で初めて網羅的に列挙し索引化し、さらに、与えられた電力品質条件を満たしつつ、かつ送電損失を最小化する最適構成を得ることに成功したのだ。
ソフトウエアの開発と専門解説書の出版
ERATOではZDDを用いて、n×nの格子グラフの対角2点間を、遠回りは良いが同じところを2度通らずに結ぶパスの総数を効率的に数え上げるというパス列挙問題(図2)の研究も実施。2013年11月には、n=26のケースにおけるパス総数数え上げを世界で初めて達成した。要した時間は1週間である。もしも素朴な方法で数え上げるとn=11の場合でも290億年かかるといわれているが、同じ問題が彼らのアルゴリズムでは数秒で解けるという。
図2
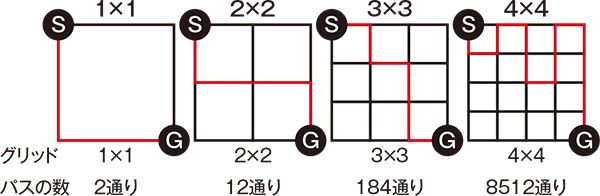
格子グラフのグリッドが増えるにつれてパスの総数は爆発的に増加する。5×5は128万2816通り、6×6は5億7578万564通りにもなってしまう。
研究で培った技術は、研究者や産業界が利用しやすい形で提供することも湊教授の目的の1つだ。パス列挙問題の研究成果は、超高速グラフ列挙索引化ソフト「Graphillion」として提供されている。またこの活用法と内部のアルゴリズム技法をまとめた専門書「超高速グラフ列挙アルゴリズム」を2015年4月に出版(森北出版)、多くの支持を得て版が重ねられている。また研究成果をもとにした選挙区割りの解析プログラムも開発されている。
ERATOの成果は、スマートグリッドや選挙区割りの最適化だけでなく、水道、ガス、鉄道、道路、通信、避難所配置などさまざまな社会インフラの解析に応用できることから、今後の活用が大いに期待されている。
