JST 課題達成型基礎研究の一環として、京都大学 大学院工学研究科の山本 量一 教授と村島 隆浩 特定助教、谷口 貴志 准教授らは、計算流体力学法と高分子動力学法の組み合わせによる「高分子流体のためのマルチスケールシミュレーション法」を用いて、円筒の周りを流れる高分子溶融体の複雑な流動挙動を再現することに成功しました。
私たちの身の回りで使われる製品は、プラスチックに代表される高分子系材料で作られています。高分子系材料は分子鎖が長く(分子量が大きく)、それらが複雑に絡み合っているため製品に十分な強度を持たせることが可能になります。プラスチック製品は、高温で溶融した高分子材料を金型に流し込む「射出成形」という方法で作られますが、金型といった複雑な流路の中で高分子が流体として、どのような挙動を示すかを理解することは、材料や製造プロセスの設計を行う際に非常に重要です。しかし、これまでは(1)工学的に重要な高分子は分子量が大きく、絡み合いがあるために高分子鎖の計算流体力学シミュレーションの計算負荷が大きいこと、(2)マクロスケールとミクロスケールを組み合わせたマルチスケールシミュレーションは、高分子鎖の状態が流れに沿って同じである場合に限られていたこと――の2点から現実の高分子材料の問題に広く適用できませんでした。
本研究チームは今回、個々の流体粒子の計算負荷を軽減するモデルで絡み合い高分子鎖をシミュレーションし、マクロな計算流体力学シミュレーションに埋め込むことで、流体とともに流れるシミュレーション法の開発に成功しました。具体的には、ミクロスケールでは複雑に絡み合った高分子液体が、マクロなスケールの円柱周りを流れる際の流動挙動の解析や予測、またミクロスケールで発生する高分子の絡み合い状態との関係を明らかにしました。今回の成果は、現実の高分子材料のマクロな流動物性を、高分子鎖のミクロな性質から直接予測可能な方法を世界で初めて提案・実装したものであり、計算科学と物質科学の両分野において非常に大きな進歩で、2012年に完成するスパコン「京」を利用することにより、大規模なシミュレーションも可能にする画期的な成果です。
今後、新機能性材料の開発や物質科学のさまざまな分野に応用できるものと期待されます。
本研究成果は、近日中に欧州の物理学雑誌「Europhysics Letters」のオンライン速報版で公開されます。
本成果は、以下の事業・研究領域・研究課題によって得られました。
戦略的創造研究推進事業 チーム型研究(CREST)
| 研究領域 |
研究領域:「マルチスケール・マルチフィジックス現象の統合シミュレーション」
(研究総括:矢川 元基 東洋大学計算力学研究センター センター長・教授) |
| 研究課題名 |
「ソフトマターの多階層/相互接続シミュレーション」 |
| 研究代表者 |
山本 量一(京都大学 大学院工学研究科 教授) |
| 研究期間 |
平成18年10月~平成24年3月 |
JSTはこの領域で、世界最先端レベルの超高速・大容量計算機環境と精緻なモデル化・統合化によって、複数の現象が相互に影響しあうようなマルチスケール・マルチフィジックス現象の高精度かつ高分解能の解を求めることを研究対象としています。上記研究課題では、ミクロ階層(原子・分子)・メソ階層(濃度分布や界面など)・マクロ階層(材料の形や製造プロセスなど)が物理的に矛盾なく相互に影響し合う画期的な多階層/相互接続シミュレーション手法を確立し、全く新しい包括的材料・プロセス設計ソフトウエアの開発を行います。
<研究の背景と経緯>
シミュレーションとは、コンピューターの中で仮想的に行う模擬実験を意味し、古くからの実験的方法や理論的方法に並ぶ新しい第3の方法に位置づけられています。身近な例では航空機やロケットなどの機体の設計や地球温暖化などの気候変動の予測にも用いられています。
この手法は、私たちの周囲にあるさまざまな物質の性質を解明する際にも極めて有効と期待されています。身近にある製品の多くは柔らかくて変形しやすい物質、つまりソフトマター(コロイドや高分子、液晶など)からできています。化粧品、日焼け止め、ヨーグルト、ゼリー、液晶テレビなどはこれらを使った代表的な製品です。また、最近のナノテクノロジーの出現によって、ソフトマターは特殊な機能を持つ新しい材料の宝庫としても注目されており、医療やエネルギー、電機、情報などさまざまな分野で今後、ますますソフトマターを利用した機能性材料が開発されることが期待されます。
ソフトマターの物性の特徴の1つは、その多くが固体的性質と流体的性質の両方を兼ね合わせていることです。固体状態ではそれを構成する原子・分子は規則的に配置されており、その流体物質は大きく変形しません。一方、流体ではそれを構成する原子・分子はランダムに動き回り、物質は自由に変形します。多くのソフトマターはこの2つの状態の中間にあり、それを構成する原子・分子は一部の規則性を残したまま、ある程度自由に動き回り、その物質の変形に対する応答も固体的な性質(弾性力注1))と流体的な性質(粘性力注2))の両方を兼ね備えます。つまり、ソフトマターでは原子・分子レベルでの構造と私たちが目にする巨視的なレベルでの変形と運動は、強い相関を持ちます。まさにこの特徴こそが機能性材料に役立つのですが、理論的・実験的研究を難しくする要因でもあります。例えば、料理で使う小麦粉や片栗粉を水で溶いたどろどろした液体(小麦粉液、片栗粉液)の流動をシミュレーションしようとすると、容器の大きさ(数センチメートル程度)よりはるかに小さなアミロースやアミロペクチンなどの高分子(数ナノメートル程度)の配置や運動を考慮しなくてはいけません。このような物質の挙動の予測に分子動力学法を用いると、途方もない計算時間が必要となります。小麦粉液や片栗粉液の流れを計算することさえ、現在の世界最速の計算機をもってしても私たちが生きている間には終わりません。コンピューターの性能向上がこの先も継続するという最も楽観的なシナリオによっても、計算が完了するのはこれから100年以上も先のことになります。
<研究の内容>
本研究グループは今回、ソフトマターのシミュレーションが抱える難題をマクロスケールとミクロスケールを組み合わせた「マルチスケールモデリング」によって解決しました。図1にシミュレーションを行った系(30cmx30cm)の略図を示します。中央に配置された円筒状の物体の直径(約6cm)は、高分子を構成する1つの原子のサイズの1024(10の24乗)倍あります。高分子溶融体の巨視的な流れは、連続体モデルの運動量保存式によって計算されます。ここで、各計算点での流速はその点での局所的な応力注3)によって変化します。通常の粘性流体(ニュートン流体注4))の場合、応力と流速の空間勾配の間に比例関係があるので、その比例定数、すなわち粘性係数さえ実験で求めておけば、各点で求めた流速から各点での応力を求め、その瞬間の流速変化を予測することができます。ところが、本研究で扱う高分子溶融体にはそのような単純な比例関係は存在しません。各計算点での応力はその点での巨視的な流速や変位だけでは表すことができず、原子・分子レベルでの高分子の配置、形状、絡み合いの状態に依存します。
そこで私たちはマルチスケールモデリング法により、この問題を解決することに取り組みました。この方法では、まず巨視的な流動を表現するために流体を多数の流体粒子で表します。この流体粒子の運動方程式を解くためには応力場を知る必要があります。この応力場を求めるために、前のステップで求めた各流体粒子の速度からその位置における局所的な変形速度(速度の勾配)を求めて、それを外場として、各流体粒子に内在する膨大な数の高分子が絡み合った状態の時間変化を粗視化高分子動力学法により計算します。この計算により求めたある流体粒子中の多数の高分子鎖の微視的情報を用いて、その流体粒子の位置における応力を統計的手法により求めます。そして全ての流体粒子の位置で求めた応力により応力場を構成し、その応力場を用いて各流体粒子の運動方程式を解き、微小時間後の全ての流体粒子の位置と速度が決まります。上記の計算を繰り返し行うことで高分子流体の時間変化が求まります。この方法を用いることで、高分子溶融体に特徴的な粘弾性注5)や履歴効果注6)を正確にシミュレーションできました。特に本研究では、微視的な状態の移流注7)を正しく取り扱うことが可能となり、任意の流動条件に対して適用可能なマルチスケール法の開発に成功しました。
図1の高分子流体中には(奥行方向については1cmの厚み分だけで考えると)約1021から1024本の高分子が存在しています。今回のマルチスケールシミュレーション法では、約108本の高分子を計算に用いているので、1013から1016分の1に計算量を節約していることになります。この膨大な計算量の節約が、微視的な情報を持った巨視的な流動の計算を可能にしています。
今回の研究では、特に重要な2つの結果が得られました。図2に、円筒状の障害物の周りを流れる高分子溶融体の速度分布、せん断速度注8)分布、せん断応力注9)分布とナビエ・ストークス方程式注10)によって計算されたニュートン流体のものとの比較を載せました。両者を比較すると、速度分布、せん断速度分布に関しては上流側(図中の黒円に対して左側)と下流側(図中の黒円に対して右側)でほぼ対称な振る舞いをしているにも関わらず、せん断応力分布は両者で大きく異なる振る舞いをしていて、高分子溶融体は上流側と下流側で非対称になっていることが分かります。これは高分子の持つ粘弾性に起因する履歴効果により応力の応答が遅れるためで、その結果、非対称な分布が生じているのです。また、円筒状の障害物の近くではせん断速度の値に比べて、せん断応力の値が小さな値を示しています。これはシアシニング注11)と呼ばれる現象で、局所的に粘度が低下していることを示しています。これも高分子流体に特有の現象であり、流動による高分子鎖の配向が生じた結果起こる現象です。単純なせん断流れの中ではワイゼンベルグ数注12)Wiが1より大きい場合にシアシニングが生じるのですが、今回のような複雑な流れの中では局所的なワイゼンベルグ数Wiが1より小さい領域でもシアシニングが生じていることが分かります。これも先ほどの履歴効果のためにシアシニングが遅れて出現しているためです。
図3に、各場所における平均的な高分子同士の絡み合い量の空間分布を示します。円筒状の物体の周囲では高分子の絡み合いが少しほぐれて、絡み合いが減った領域が下流側に広がっていることが分かります。このような巨視的な流動中の微視的な物理量の空間分布は、従来の計算手法や現在の最新の計測技術でも測定することが困難な情報で、本マルチスケールシミュレーション法の計算によって、世界で初めて定量的に示すことができました。
<今後の展開>
今回開発した、計算流体力学法と高分子動力学法のハイブリッドによるマルチスケールシミュレーション法は、目に見える巨視的な流動と原子・分子レベルの微視的な配置や形状と、絡み合いの状態を直接関係づけて計算することに成功しました。その結果、今までの計算手法では知ることができなかった高分子同士の絡み合い量の空間分布を知ることできました。また、今回のマルチスケールシミュレーション法は任意の流動条件に対して適用可能な方法であり、実験では調べることが困難な微視的な情報を解析できるので、新機能性材料の開発や物質科学のさまざまな分野に応用できるものと期待されます。
シミュレーション科学の発展は、激しい競争を繰り広げているコンピューターの技術革新に大きく支えられています。しかし、最先端のスーパーコンピューターも、その性能を十分に引き出すことができるソフトウエアがなければ無用の長物に過ぎません。
マルチスケールシミュレーション法は、通常の分子動力学法とは異なり、膨大なCPUを持つコンピューターとの相性が極めて高いという特徴も持っています。これは、計算負荷の最も高い分子動力学法による計算部分が各計算点で独立であるため、計算の並列実行が容易であることに起因しています。この方法を「京」のような膨大なCPUを持つコンピューターで用いることにより、分子数が100億個にも達する世界最大規模の分子動力学シミュレーションの実現が期待されます。
<参考図>
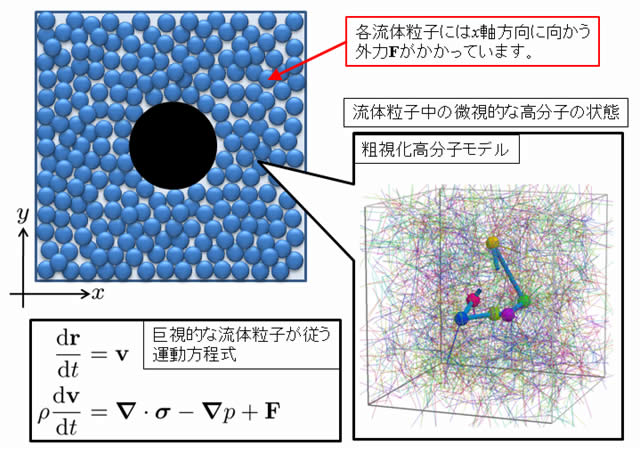
図1 問題の概略図
流体は流体粒子として扱い、流体粒子の運動方程式を解きます。また各流体粒子の応力は、流体粒子に関連づけられた粗視化高分子モデルにおいて計算します。図の中央の黒円は円筒を真上から見ているところを表しています。黄色の矢印は流体粒子の流れの方向を示しています。
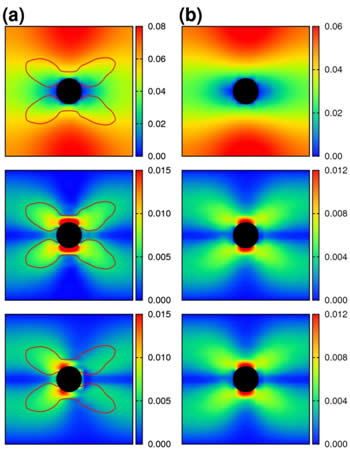
図2 円筒状の障害物の周りの流れ
(a)高分子溶融体の挙動。(b)ニュートン流体の挙動。上から流速分布、せん断速度分布、せん断応力分布。図の値は適当な量で無次元化された絶対値を表しています。(a)図中の赤色の線で囲われた内側の領域は、局所的なワイゼンベルグ数Wiの値が1より大きい領域です。黄色の矢印は流れの方向を示しています。
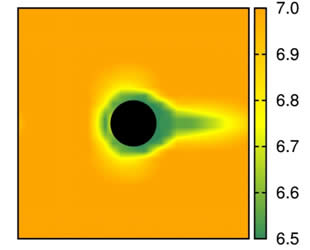
図3 流動中の絡み合い量の空間分布
高分子同士の絡み合いが流動中にどのように変化するかを調べた図。円筒の周囲とその下流側(円筒の右側)で絡み合いが弱まっているのが分かります。黄色の矢印は流れの方向を示しています。
<用語解説>
- 注1) 弾性力
- 固体の変形の大きさに比例する力。
- 注2) 粘性力
- 流体の変形の速さに比例する力。
- 注3) 応力
- 物体内部に考えた任意の単位面積を通して、その両側の物体部分が互いに相手に及ぼす力をその面に関する応力と称します。
- 注4) ニュートン流体
- 応力と変形速度の間に単純な比例関係がある流体。
- 注5) 粘弾性
- 高分子溶融体などが粘性力と弾性力の両方を有する性質のこと。
- 注6) 履歴効果
- 過去に経験した運動の履歴によって応力と変形の関係が変わること。
- 注7) 移流
- 空間内の物質が、流動によって運ばれること。
- 注8) せん断速度
- ずり速度。流動方向(x軸方向)の速度Vxの、流動方向と垂直な方向(y軸方向)に対する勾配。
- 注9) せん断応力
- 流体中で微小な立方体を考えた時に、流動方向(x軸方向)に平行な面を平行方向にすべらせるように働く応力。
- 注10) ナビエ・ストークス方程式
- ニュートン流体(注4参照)の運動を表現する方程式。
- 注11) シアシニング
- せん断速度が大きくなると粘度が低下する現象。
- 注12) ワイゼンベルグ数
- せん断速度と高分子の緩和時間を掛けた無次元数。一般にワイゼンベルグ数が1より大きいとシアシニング(注11参照)を示す。
<論文名および著者名>
“Multiscale simulation of history dependent flow in entangled polymer melt”
(高分子溶融体中における履歴依存流動のマルチスケールシミュレーション)
doi: 10.1209/0295-5075/96/18002
<お問い合わせ先>
<研究に関すること>
村島 隆浩(ムラシマ タカヒロ)
京都大学 大学院工学研究科 化学工学専攻 特定助教
〒615-8510 京都府京都市西京区京都大学桂
Tel:075-383-2671 Fax:075-383-2651
E-mail:
谷口 貴志(タニグチ タカシ)
京都大学 大学院工学研究科 化学工学専攻 准教授
〒615-8510 京都府京都市西京区京都大学桂
Tel:075-383-2681 Fax:075-383-2651
E-mail:
山本 量一(ヤマモト リョウイチ)
京都大学 大学院工学研究科 化学工学専攻 教授
〒615-8510 京都府京都市西京区京都大学桂
Tel:075-383-2661 Fax:075-383-2651
E-mail:
<JSTの事業に関すること>
石井 哲也(イシイ テツヤ)
科学技術振興機構 イノベーション推進本部 研究領域総合運営部
〒102-0075 東京都千代田区 三番町5三番町ビル
Tel:03-3512-3524 Fax:03-3222-2064
E-mail: