ポイント
- 「切り紙」の高い伸長性の鍵が、平面内変形から平面外変形への転移現象にあることを見いだした。
- 「切り紙」が持つ高い伸長性の物理原理をシンプルな数式で説明することに成功した。
- 発見された数式は、切り紙構造を応用展開する際の明確な指導原理を与える。
内閣府 総合科学技術・イノベーション会議が主導する革新的研究開発推進プログラム(ImPACT)の伊藤 耕三 プログラム・マネージャーの研究開発プログラムの一環として、お茶の水女子大学の奥村 剛 教授は磯部 翠 大学院生と共に、「切り紙注1)」の構造が持つ高い伸長性の鍵が、平面内変形(二次元的な平らな状態を維持したままの変形)から平面外変形(三次元的な立体的な構造を取る変形)への転移現象(突然の変化)にあることを見いだし、その物理原理をシンプルな数式で表すことに成功しました。
「切り紙」構造は、シート状物質に規則的に穴を配置した構造で、引っ張ることで柔軟に変化し立体的な構造を創り出すことができます。私達に身近な例としては、ワインボトルなどにかぶせる緩衝材があります。この構造は、フレキシブルな電極や太陽電池などのさまざまな工学応用の鍵として期待され、最近、急速に世界の注目を集めてきており、今後、再生医療では細胞シート注2)への展開も期待されます。
今回、奥村らは、「切り紙」の柔らかさを表す量(弾性率)と「切り紙」が平面内変形から平面外変形に転移する条件を、シンプルで美しい数式により表すことに成功しました。シンプルでありながら実験データと良く整合性を持ち、特に平面内変形の場合の弾性率の式と転移の条件式は極めて精度良く成立していることが分かりました。これらの数式は、切り紙構造を応用展開する際の明確な指導原理となります。今後、最先端の自動車技術としてリチウムイオン電池注3)などに組み込まれる多孔性ポリマーシートの強靭化などへの展開が期待されます。
本成果の一部は、2016年4月27日10時(英国時間)発行の英国科学誌「Scientific Reports」に掲載されます。
本成果は、以下のプログラム・研究開発課題によって得られました。

奥村 剛 教授
内閣府 革新的研究開発推進プログラム(ImPACT) https://www.jst.go.jp/impact/
| プログラム・マネージャー |
伊藤 耕三 |
| 研究開発プログラム |
超薄膜化・強靱化「しなやかなタフポリマー」の実現 |
| 研究開発課題 |
印象派物理学によるタフポリマー開発の指導原理の構築 |
| 研究開発責任者 |
奥村 剛(お茶の水女子大学 基幹研究院 教授) |
| 研究期間 |
平成26年10月~平成30年3月 |
枝葉末節を排しシンプルに対象を捉えることでそのものの本質を鮮明に描き出そうという印象派物理学注4)の手法がソフトマター注5)の分野で注目されていますが、本研究開発課題では、この印象派物理の手法に基づき、多孔性高分子薄膜の強靱化や、高分子材料の強靱性に深く関わる粘性散逸の問題等に取り組んでいます。
<伊藤 耕三 プログラム・マネージャーのコメント>
本チームでは、複雑な現象の本質をシンプルに捉える印象派物理学という新しい技術を用いて、しなやかでタフなポリマーの材料設計の指針を開発しています。今回の成果は、「切り紙」が持つ高い伸長性を理論的に解析することで、切り紙構造をタフポリマーに応用する際の指導原理を確立したもので、リチウムイオン電池用セパレータなど多孔膜への展開や、医療分野など幅広い分野への応用が期待される基礎技術として期待されます。
<研究の背景と経緯>
強靭な天然物質の研究を展開してきた奥村教授のグループは、ImPACT伊藤プログラムにおいて、多孔性ポリマーシートの強靭化に関連する基盤技術などの研究を行ってきました。これからの自動車技術を支えるリチウムイオン電池の性能を向上させるためには、内部に組み込まれる多孔性ポリマーシートの厚みを薄くかつ丈夫にすることが求められています。一方、自然界には、多孔性の構造を取ることで強度を増している物質があります。例えば、日本でお酒の友としても親しみのあるナマコはその海面組織が多孔性構造を取ることで、あの弾力性に富んだ歯ごたえのある強靭性が生み出されています。これらの背景から、奥村教授らは、ImPACT伊藤プログラムの基盤技術に関わる研究として多孔性物質の研究を展開してきており、その1つのテーマとして切り紙構造の研究に取り組んできました。研究の発端は、スーパーマーケットなどで購入したワインが割れないように保護するためにボトルにかぶせる紙製の緩衝材(図1)にヒントを得た奥村教授が、約2年半前に研究室に仮配属された磯部 翠 氏(現修士2年生)とともに始めた実験でした。
日本では多くの人に親しみのある切り紙構造(図1(a)、(b))に関しては、ここ1~2年世界でさまざまな工学的応用研究が爆発的な速度で発展して来ています。例えば、「切り紙」を用いて、大きな伸長性を持つ電極やバッテリー、太陽電池が実現されたり、グラフェンシート注6)を「切り紙構造」によって柔らかくすることで極微のスケールで電磁式アクチュエータが作られたりしています。しかし、物理原理を明らかにする研究はほとんど手つかずの状況にありました。
<研究の内容>
奥村教授は磯部氏とともに、ソフトマター物理学の分野で注目されている印象派物理学の手法に基づいて、ワインボトルにかぶせる切り紙を、物理的本質を損なわずに単純化した切り紙パターン(図2(a))に着目しました。そして、実験と理論の両面から研究を進めた結果、最近の応用研究で注目されている切り紙構造の高い伸長性が、平面内変形から平面外変形への転移現象のおかげで実現していることに気づきました(図2(b)、(c))。この事実を基に、彼らは、この転移現象を記述する物理モデルを構築しました。その結果、(1)切り紙が少しだけ引っ張られた場合(平面内変形)と(2)大きく引っ張られた場合(平面外変形)のそれぞれに、切り紙の柔らかさを表す量(弾性率)を数式で表すことに成功しました。さらに、(3)平面内から平面外の転移が起こる条件も数式で表しました。この条件は、「切り紙」の弾性率を表す2つの数式が入れ替わる転移条件に相当し、これによって転移点での「切り紙」の伸びを知ることができます。
また、(1)~(3)に対応した3つの数式は実験データと良く整合性を持つことが分かりました。特に(1)と(3)に相当する、平面内変形の場合の弾性率を表す式と転移点の伸びを表す式は極めて精度よく成立していることが分かりました。こうして、確立された物理法則を表す数式は、いずれも驚くほどにシンプルであるため(図3)、今後の工学的応用などの技術開発の指導原理として役立つことが期待されます。
<今後の展開>
本研究は、物理学と工学の知見を融合して応用研究を展開しています。本研究は物理が専門の奥村教授のグループで行われてきましたが、最近、工学部出身の武居 淳 氏(お茶の水女子大 特任助教)が本研究に加わって、応用展開を開始しています。紙を始めとして、ゴムやプラスティックなどのポリマー系の材料で研究を進めることで、材質に関わらず、本研究で発見された法則がさまざまな物質に共通に当てはまることを確認し、具体的な応用例を示しています(特許出願済み)。
例えば、最近、再生医療分野で注目を集める細胞シートにこの切り紙構造を応用すれば、患者の被移植部位の状態に合わせた弾性率を持たせることで、手術の成功確率を上げるメリットも期待されます。ワインボトルの緩衝材のように円筒形状で応用すれば(図1(a))、弾性率可変の医療・スポーツ用のサポーターなどへの応用も期待できます。また平面内の変形から平面外の変形への転移現象は、検出が容易です。このため、この転移点を利用した、力を感知するデバイス(フォースセンサー)の開発も期待できます。グラフェンシートなどで作成すれば、ごく微弱な力を測定するセンサーの作製も可能と考えられます。
<参考図>

図1 日本で身近に使われる切り紙の例
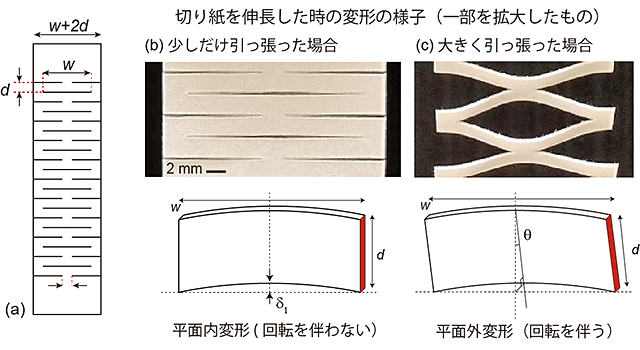
図2

図3 本研究で示された切り紙構造の高い伸長性の物理的本質を表すシンプルな3つの数式
弾性率は、「切り紙」の柔らかさを表す量であり、「ひずみ」は切り紙ののびを表す量。d、h、wは図2(a)に定義された切り紙のパターンを表す量(hはシートの厚さ)。Eはもともとの素材(例えば紙)の弾性率(α、β、γは数値係数)。
<用語解説>
- 注1) 切り紙
- 紙にさまざまなパターンで切り込みを入れることで、さまざまな形を実現する伝統工芸技術。特に、立体的な形を実現することも行われてきた日本の「切り紙」という言葉が、最近の工学・科学分野では、折り紙と同様に非常によく用いられる。
- 注2) 細胞シート
- 再生医療は、人体の組織が損傷しその機能を失った場合に、例えば、幹細胞と呼ばれる細胞のたねのような細胞が持つ自己修復性を使って、損傷した組織の機能を回復する技術。細胞シートは、細胞をシート状にして細胞間の接着や組織機構を再建させた細胞の集合体。細胞シートを、さまざまな臓器に張り、その部位に生着させることで、移植治療ができるようになると期待されている。特に、角膜や心筋を対象に臨床応用も始まり、再生医療への道を拓く技術として期待されている。
- 注3) リチウムイオン電池
- 板状の電極を多孔性のポリマーシートで仕切り、それをユニットとして積層することで性能が向上する電池。これらの電池の積層効率を上げるためには、薄くて丈夫な多孔性ポリマーシートが欠かせない。このためにタフでしなやかな多孔性ポリマーのシートの開発は、これからの自動車技術の要となる重要な研究課題である。
- 注4) 印象派物理学
- 1991年にノーベル物理学賞を受賞した故ドゥジェンヌ博士が提唱した研究手法で、物理の研究を印象派絵画に例え、枝葉末節を意識的に排除し、シンプルに情景(物理)を捉えることで、その美的(物理的)本質をより鮮明に浮かび上がらせようとするもの。今後この手法でさまざまな分野で研究が進むことで、企業の開発現場などで指導原理として役に立つ原理が次々と明らかになって行く可能性がある。
- 注5) ソフトマター(あるいは、ソフトマター物理学)
- 固体と液体の中間のような性質を持つ高分子・液晶・コロイド、さらには、粉粒体などを含む物質群、あるいは、それらを研究対象とする物理学の一分野。ドゥジェンヌ博士がソフトマターというタイトルでノーベル賞受賞講演を行ったことから定着した。
- 注6) グラフェンシート
- 炭素原子が蜂の巣のような六角格子に配列されたシートで、その厚みは炭素原子一個分の厚みしかない。電気的性質に優れ、薄くてしなやかで透明なため、さまざまな電気的デバイス(例えば、タッチパネル)への応用も期待される。初めてグラフェンの単離に成功したガイム博士とノボセロフ博士は、その功績で2010年度のノーベル物理学賞を受賞している。
<論文情報>
| タイトル |
“Initial rigid response and softening transition of highly stretchable kirigami sheet materials.”
(高い伸長性を持つ切り紙シート物質における初期の硬い応答と軟化転移) |
| 著者名 |
Midori Isobe and Ko Okumura(Graduate School of Ochanomizu University, Ochanomizu University)(磯部 翠(お茶の水女子大学 大学院)、奥村 剛(お茶の水女子大学)) |
| 掲載誌 |
Scientific Reports |
| doi |
10.1038/srep24758 |
<お問い合わせ先>
<研究に関すること>
奥村 剛
お茶の水女子大学 基幹研究院 教授
〒112-8610 東京都文京区大塚2-1-1
Tel:03-5978-5321 Fax:03-5978-5321
E-mail:
<ImPACTの事業に関すること>
内閣府 革新的研究開発推進プログラム担当室
〒100-8914 東京都千代田区永田町1-6-1
Tel:03-6257-1339
<ImPACTプログラムに関すること>
科学技術振興機構 革新的研究開発推進室
〒102-0076 東京都千代田区五番町7 K’s五番町
Tel:03-6380-9012 Fax:03-6380-8263
E-mail:
<報道担当>
お茶の水女子大学 企画戦略課 広報担当
〒112-8610 東京都文京区大塚2-1-1
Tel:03-5978-5105
E-mail:
科学技術振興機構 広報課
〒102-8666 東京都千代田区四番町5番地3
Tel:03-5214-8404 Fax:03-5214-8432
E-mail: