ポイント
- 「京」の全計算プロセッサを利用した世界最大規模の固有値計算に成功
- 半導体や新材料の開発などのシミュレーションがより大規模化・高速計算が可能に
- 大規模シミュレーションを実現するソフトウエア「EigenExa」を公開
理化学研究所(理研、野依 良治 理事長)は、大規模コンピュータシミュレーションや、ビッグデータにおけるデータ相関関係の解析などに必要な行列注1)の固有値を高速で計算できるソフトウエア「EigenExa(アイゲンエクサ)」を開発しました。EigenExaを用い、スーパーコンピュータ「京」注2)で100万×100万の行列での固有値計算を行った結果、これまで1週間程度必要だと考えられていた計算を、わずか1時間で計算することに成功しました。これは、理研計算科学研究機構(平尾 公彦 機構長)大規模並列数値計算技術研究チーム(今村 俊幸 チームリーダー)を中心とする研究チームによる成果です。
複雑な方程式を数値的に解く計算科学分野では大きなサイズの行列の固有値を求める(行列の対角化注3))ことを頻繁に行います。この手法は、半導体デバイス設計や新材料開発、新薬の探索などを行うための大規模コンピュータシミュレーションや、バイオインフォマティクスや社会科学などで用いられるデータ相関関係の解析などによく使われます。しかし、行列の固有値計算は、その計算量が行列の次元(1行当たりの要素の個数)の3乗に比例して増加するため、これまでのコンピュータでは能力不足でした。「京」の登場によりコンピュータの能力不足の面は大幅に改善されましたが、「京」の能力を生かし切る固有値計算用の数学ソフトウエアは存在しませんでした。そのため、大規模な固有値問題は非常に難しい問題の1つでした。
行列の固有値計算では、いったん行列を固有値計算が行いやすい形に変換し、それを中間形式として取り扱います。通常、中間形式としては帯行列注4)(ゼロでない要素が対角線上に帯状に分布する行列)が採用されます。本研究チームはこれまでの変換アルゴリズムとは全く異なる新しい計算アルゴリズムを考案し、それを基にEigenExaを開発しました。今回、「京」の全663,552プロセッサ(理論ピーク性能10.6ペタFLOPS)とEigenExaを用いて計算し、世界最大規模の100万×100万の密行列注5)(行列を構成する要素がゼロでない行列)の固有値を求める計算が1時間以内で可能なことを確認しました。この時の「京」での実効速度は1.7ペタFLOPS(理論ピーク性能比16%に相当)という極めて高い数値を記録しました。EigenExaは2013年8月1日より、オープンソースソフトウエアとして一般に公開されています。
本研究の一部は、科学技術振興機構(JST) 戦略的創造研究推進事業 CRESTの一環として行われました。
1.背 景
行列の固有値計算(行列の対角化)は、半導体設計や未知の性質を持つ材料の開発、新薬設計などのための大規模なコンピュータシミュレーションや、ビッグデータにおけるデータ相関関係の解析などで必ず使用される計算法です。特に、コンピュータシミュレーションで行われる行列の固有値計算の大部分は、行列の左上から右下への対角線を基準に対称な行列で、かつ全ての要素が実数である実対称行列注6)の標準固有値問題注7)あるいは一般化固有値問題注7)と呼ばれるものです。大規模な問題では行列の次元(縦横のサイズ)は数万から数十万になります。
行列の標準固有値問題や一般化固有値問題は、行列の1行当たりの要素数の3乗に比例して計算量が増加することが知られています。要素数が2倍になれば計算量は8倍になるということです。小規模な問題を扱う場合には一般的なコンピュータでもわずかな時間で計算できますが、問題サイズが数倍になるだけで計算することが難しくなります。計算時間の削減のためには、「京」のような高い計算能力のスパコンを利用することが必要です。
また、固有値計算では専門的な数学の知識が必要になるため、専用の数学ソフトウエアを利用することが一般的です。しかし、現在のスパコンで利用されている標準的な数学ソフトウエアは1990年代後半のスパコンをベースに設計・開発されているため、「京」のような超並列コンピュータを想定して開発されていません。また、こうした標準数学ソフトは、新しいプロセッサ技術の登場や、さまざまなプログラミング言語が利用されている現在では、最先端のソフトウエアとは言えなくなりつつあります。したがって、最新鋭のコンピュータの能力を生かすためには、最先端のハードウエアを分析し、それに適した計算アルゴリズムを採用した新しいソフトウエアを新たに開発する必要があります。
固有値計算は多くのシミュレーションで必要不可欠です。しかし、計算時間がかかるために大規模問題を高速に計算することが難しい問題の1つでした。そのため、これまでは近似や問題サイズを小さくするなどして大規模な固有値問題の計算を避ける傾向がありました。しかし、1秒間に1京回以上の浮動小数点計算が可能な超並列のスパコンが続々と出現している現在、その計算能力を活用してより大規模な固有値計算を高速に計算するソフトウエアへの要求が高まっています。さらに、それを実現するソフトウエアがフリーソフトウエアとして広く公開されることが、計算科学分野と産業界の双方の研究者から期待されています。
2.研究手法と成果
一般的に固有値の計算は行列をより固有値計算が行いやすい行列に変換し、それを中間形式として取り扱います。従来の計算アルゴリズムは、①行列を構成する要素がゼロでない行列である密行列を、三重対角行列注4)(帯行列の中で行列の対角線上の要素とその上下にゼロでない要素がある行列)に変換する前処理を行います。②その後に、三重対角行列の固有値計算を解き、固有値と対応する固有ベクトル注4)を計算します。③最後に、もとの行列の固有ベクトルにするための後処理を行います。図の緑線部分はこの3段階の流れを示しています。しかし、三重対角行列に変換する前処理が、最も計算時間を必要とする部分であることが、固有値計算の問題となっています。
この問題への解決方法として、前処理として一度、帯行列に変換し、さらに三重対角行列に変換する2段階のスキームとする手法(図の青線部分)も開発されました。しかし、この2段階スキームは前処理部分を高速化できますが、後処理部分の計算量が2倍以上に増加するため、固有ベクトルの計算も含めた新しいスキームの開発が進みませんでした。
そこで、研究チームでは、前処理に三重対角行列を経ずに、直接帯行列を経由して固有値と固有ベクトルを求めるアルゴリズムを採用した「新しい1段階スキーム」に基づいた固有値計算ソフトウエア「EigenExa」を開発しました(図の赤線部分)。新しい1段階スキームでは、前処理は2段階スキームに類似した性質を持ち、後処理は今までの古い1段階スキームと同じ性質を持ちます。また、固有値計算部分は三重対角行列を計算する場合に比べて数倍増加しますが、前処理での処理時間削減の効果が大きいため、新しい1段階スキーム全体はより少ない計算時間となります。図の左右にある薄黄色と薄青色で塗りつぶした三角形の部分がそれぞれ前処理、後処理に対応しています。
研究チームは、EigenExaを2013年8月1日、オープンソースソフトウエアとして一般に公開しました。EigenExaは大規模並列数値計算技術研究チームのホームページ(http://www.aics.riken.jp/labs/lpnctrt/index.html)からダウンロードできます。すでに「京」にもインストールされ、「京」のアカウントを持つユーザであれば誰でも利用できます。
2013年8月に行われた「京」の大規模ジョブ実行では、「京」の全663,552プロセッサ(理論ピーク性能10.6ペタFLOPS=1秒間に1京600兆回の浮動小数点計算をする能力)でのEigenExaの動作確認と性能測定を行いました。「京」の計算用プロセッサの全てを使用するため、対象となる問題も世界最大規模の100万×100万までの数字がランダムに並んだ密行列を用いました。
測定の結果、100万×100万の行列の固有値計算が約1時間で完了することを確認しました。その際の処理の実行速度は「京」の理論ピーク性能の16%に当たる1.7ペタFLOPSという極めて高い数値でした。固有値計算は遠距離にあるプロセッサ同士の通信を必要とするため高い性能が得られにくいのですが、この実行速度は隣接するプロセッサ間などの単純な通信で構成される大規模シミュレーションが記録する数値と同等のものです。国内に存在する100テラFLOPS級のスパコンを使っても、1週間程度の占有利用をしなければ計算できない問題が1時間程度で計算可能になったことは極めて画期的といえます。
また、この規模の固有値計算が可能なスパコンは世界に数台ありますが、100万×100万の行列の固有値問題が計算されたという報告はこれまでにありません。過去の世界最大規模の固有値計算として、地球シミュレータ注8)の4,992プロセッサを用いて40万×40万行列を3時間半で行った記録がありますが、EigenExaはそれを大幅に上回る大規模な計算に成功しています。
コンピュータシミュレーションでは固有値計算のような基本部分の計算に1時間以上要する場合は、現実的な問題サイズとは判断されません。今回の計算結果は、「京」の高い計算能力と高性能なEigenExaの利用により、数十万から100万程度の固有値問題は1時間弱で計算が可能であり、現実的なコンピュータシュミレーションに活用できることを示しています。
3.今後の期待
今回の研究開発により、「京」においては、数万×数万から100万×100万の行列の固有値計算はごく普通の計算の範疇に入ることが立証されました。つまり、シミュレーションの中でより大規模な問題に対して固有値計算を実行できます。また、これまでの計算手法を比べて、同じ規模の行列であれば、より高い計算精度で求めることができるようになります。現在「京」で固有値計算を実施している主な分野には量子物理や量子化学があります。今回の研究成果を応用することで、今後、多くのシミュレーションの規模を大幅に拡大することが可能となります。例えば、数万原子からなる大規模な分子の量子化学計算では通常省略される全系軌道計算が短時間にできるようになり、反応性などのより詳細な議論が可能となります。他にも、新物質の性質を調べるための大規模な量子スピン系の3次元シミュレーションが可能になります。これらを通じて、半導体デバイス設計や新材料開発、新薬設計に大きく貢献すると期待できます。
なお本研究の一部は、JST 戦略的創造研究推進事業 CREST「ポストペタスケール高性能計算に資するシステムソフトウェア技術の創出」(研究総括:米澤 明憲(独立行政法人 理化学研究所 計算科学研究機構))における研究課題「ポストペタスケールに対応した階層モデルによる超並列固有値解析エンジンの開発」(研究代表者:櫻井 鉄也 筑波大学 大学院、共同研究者:今村 俊幸)の一環として行われました。
<参考図>
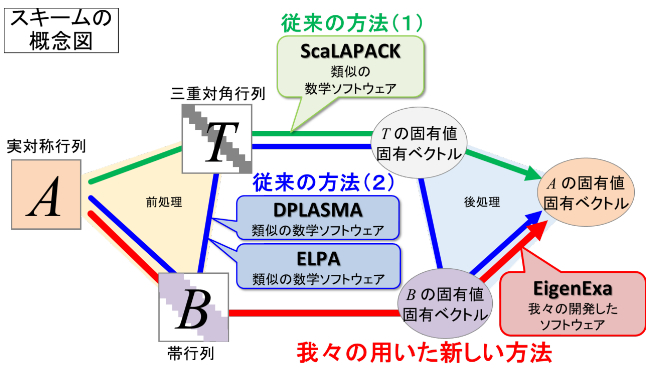
今回考案した「新しい1段階スキーム」
新しい1段階スキーム(赤線)では、前処理は2段階スキーム(青線)に類似した性質を持ち、後処理は今までの古い1段階スキーム(緑線)と同じ性質を持つ。また、固有値計算部分は三重対角行列を計算する場合に比べて数倍増加するが、前処理での処理時間削減の効果が大きいため、新しい1段階スキーム全体はより少ない計算時間となる。左右にある薄黄色と薄青色で塗りつぶした三角形の部分はそれぞれ前処理、後処理に対応している。
<用語解説>
- 注1) 行列
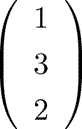
- いくつかの数字を同時に扱うために、数字を縦に並べてできる数字の集まりを「ベクトル」と呼ぶ。ベクトルはコンピュータシミュレーションで扱う多数の情報からなる抽象的なデータとして欠かすことができないもので、ベクトル同士の足し算や定数倍などの演算を行う。また、ベクトルを構成する数字の個数をベクトルの「次元」と呼ぶ。
-
ベクトルの例:3個の数字なので3次元のベクトル
「行列」は、数字を縦横に並べてできる数字の集まり。同じ次元のベクトルを横に並べたものも考えることができる。本研究では縦横が同サイズの正方行列を扱い、○×○の行列と呼び、行列の次元を○と記述している。
行列の例:3×3の行列、3次元の行列
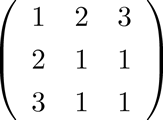
-
行列内のベクトルと対応する位置のベクトル内の数字とを定数倍して足し合わせてできるベクトルを行列とベクトルの積と定義する。このベクトルをさらに横に並べることで、行列と行列の積が定義される。
行列とベクトルの積の例:
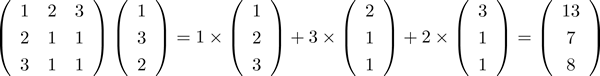
- 注2) スーパーコンピュータ「京」
- 文部科学省が推進する「革新的ハイパフォーマンス・コンピューティング・インフラ(HPCI)の構築」プログラムの中核システムとして、理研と富士通が共同で開発を行い、2012年9月に共用を開始した計算速度10ペタFLOPS級のスーパーコンピュータ。
- 注3) 行列の対角化
- 行列の対角化とは、行列の固有値計算のこと。線形代数の基本計算の中に行列の固有値計算がある。数式を使って行列をA、ベクトルをxと記述する。この時、行列Aとベクトルxとの積yを次のように書くことにする。
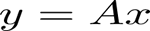
ここでxをうまく選べば、yがxの定数λ倍となる場合がある。
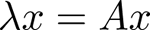
このような関係を満足する定数λを行列Aの固有値、xを固有ベクトルと呼ぶ。
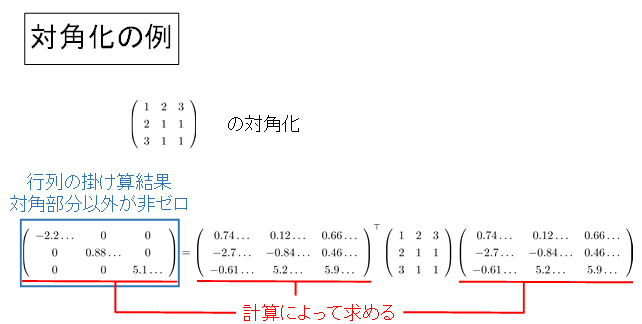
行列Aは行列の次元と同じ数だけの固有値を持ち、ある性質を持つ行列の場合は次元と同じ数の固有ベクトルを持つ。このときに、固有ベクトルを並べてできる行列をX、固有値を対角線上に並べ、それ以外を0とした行列をΛと書くと
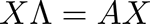
-
という関係が成り立つ。例に挙げたような、対角線を基準にして対称な行列(対称行列と呼ぶ)の場合には、さらに、上の関係式の左から Xの行と列を入れ替えてできる行列Xt(Xの転置行列と呼ぶ)を掛けて、次のような関係になることが数学的に知られている。

ここで、Λは行列の対角線上に0でない値が並ぶため対角行列と呼ばれる。この式は、固有値計算で固有値Λと固有ベクトルXを計算すれば、元の行列Aを対角行列に変換できることを示している。このことから、「行列の固有値計算」は「行列の対角化」と呼ばれることがある。
-
- 注4) 帯行列・対角行列・三重対角行列
- 帯行列の例:対角線からその上下にもゼロでない要素が帯状に分布する行列。5×5の行列

-
対角行列の例:行列の左上から右下への対角線上にのみゼロでない値があり、それ以外の要素が全てゼロとなっている行列。5×5の行列
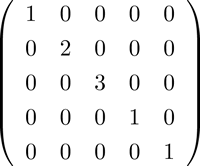
- 三重対角行列の例:帯行列の中で対角線上の要素に加えてその上下にゼロでない要素がある行列。ある範囲に存在する固有値の個数が簡単に分かるなどの特質を持つ。
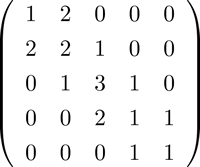
- 注5) 密行列
- 行列の要素がゼロでない行列、または、ゼロであっても全ての要素を使って行列の計算など扱うときに「密行列」と呼ぶ。一方、要素の多くがゼロであり、ゼロでない非ゼロ要素の個数が少ない行列を「疎行列」と呼ぶ。疎行列では、非ゼロ要素のみを使って行列を表現し、行列とベクトルの積計算を行う。
- 注6) 実対称行列
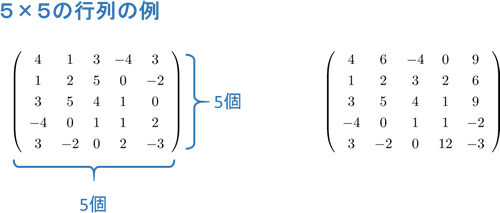
- 行列の左上から右下への対角線上を基準にして対称な行列を対称行列といい、全ての要素が実数のものを実対称行列という。下の図は5×5の行列の例(左:対称行列、右:非対称行列)。
- 注7) 標準固有値問題・一般化固有値問題
-
標準固有値問題は
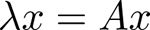
の形をしているが、左辺がベクトルxという形ではなく行列Bを乗じた式。
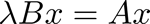
を満足するようなλとベクトルxを求める問題を一般化固有値問題と呼ぶ。
- 注8) 地球シミュレータ
- 地球規模の気象変動予測を目的として科学技術庁(1998年度当時)が2002年に開発した計算速度40.96テラFLOPSの当時世界最速のスーパーコンピュータ。
<お問い合わせ先>
<研究に関すること>
独立行政法人 理化学研究所 計算科学研究機構 大規模並列数値計算技術研究チーム チームリーダー
今村 俊幸(いまむら としゆき)
Tel:078-940-5832 Fax:078-599-6767
計算科学研究機構 広報国際室
岡田 昭彦(おかだ あきひこ)
Tel:078-940-5625 Fax:078-304-4964
E-mail:
<報道担当>
独立行政法人 理化学研究所 広報室 報道担当
Tel:048-467-9272 Fax:048-462-4715
独立行政法人 科学技術振興機構 広報課
Tel:03-5214-8404 Fax:03-5214-8432